Question 364906: 2x^2/3 - 8x^1/3 + 15 = 0
Thanks for your help and time!!!
Found 2 solutions by Jk22, jsmallt9:
Answer by Jk22(389)   (Show Source):
Answer by jsmallt9(3758)  (Show Source):
You can put this solution on YOUR website! Note: Please put fractional exponents in parentheses. Without them it is difficult to distinguish whether the exponents are fractions or whether the entire terms are fractions:
 (without parentheses)
or
 (with parentheses)
Tutors are more like ly to help if the problem is clear.
I am going to assume that the second equation is the correct one. The key to solving this equation is noticing that the first exponent, 2/3, is twice the second exponent, 1/3. Since raising powers to a power means we multiply exponents, an exponent that is twice another exponent represents the square of that other exponent. Using a temporary variable may help make this clear:
Let q =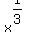 
Then 
Substituting these into the equation we get:
Looking at the equation this way we can see that it is quadratic. This make the original equation in quadratic form for 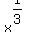. We can use techniques for solving quadratic equations to solve this.
This equation does not factor. (Are you sure about the "2" in front? Maybe this is actually problem #2 and the equation is really  ? I ask because without the two, the equation does factor and we get some nice simple solutions. With the 2 the problem is more difficult to solve.)
Since the equation, as you posted it does not factor, we must resort to the quadratic formula:
Simplifying we get:
Since the radicand (the expression within a radical) of the square root is negative, we can see that this equation has no solutions within the set of real numbers. And this means that the original equation also has no solutions within the set of real numbers.
If the leading 2 is correct and if you are only looking for real solutions, this is the end of the problem. I will continue to provide a) complex solution(s) and b) a solution without the leading 2.
Complex solution.
We have found that
we will rewrite this using  :
Now we'll simplify  :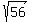
Now we'll reduce the fraction. Factoring out a 2 in the numerator and denominator we get:
The 2's cancel:
leaving:
Rewriting this in a + bi form we get:
These are complex solutions for q. However we want solutions for x. So we substitute back in for q:
To solve this we just cube each side. But first let's write separate equations for each solution:
 or 
Now we cube:
 or 
On the left side the cubing is simple. We just multiply the exponents. On the right side, we must use either the Binomial Theorem or multiply out  by hand. I'll use the Binomial Theorem:
 or 
 or 
Since  and  this becomes:
 or 
which simplifies to:
 or 
which in a + bi form is:
 or 
Simplifying the coefficients of i we get:
 or 
 or 
which are the complex solutions to the original equation (as posted).
Without the leading 2.
Then the equation becomes
This will factor nicely:
{q - 3)(q - 5) = 0
From the Zero Product Property we know that this product is zero only if one of the factors is zero. So:
q - 3 = 0 or q - 5 = 0
Solving these we get:
q = 3 or q = 5
Substituting back in for q we get:
 or 
Cubing each side we get:
x = 27 or x = 125
Once you have done a few of these "quadratic form" equations, you will no longer need a temporary variable. You will be see how to go directly from
to
etc.
|
|
|
