SOLUTION: A friend of mine told me that if you need help with algebra this was the website to submit your question. I am confused on what steps to take the get the final answer. If someone c

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: A friend of mine told me that if you need help with algebra this was the website to submit your question. I am confused on what steps to take the get the final answer. If someone c      Log On


   

Question 362564: A friend of mine told me that if you need help with algebra this was the website to submit your question. I am confused on what steps to take the get the final answer. If someone could be so kind as to show me what to do, I would be appreciate it. I know it's time consuming, but could you please work the problem in all vital steps (maybe with some direction) so I know how to complete the next series that I have to do for my assignment?
11.4, #9
Directions: Solve the equation by making an appropriate substitution.
x^(-2)+〖8x〗^(-1)=-10 (should be x - squared, and 8x to -1 power)

Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
(should be x - squared, and 8x to -1 power)
----------------------
x%5E-2+%2B+8x%5E-1+=+-10
-----------
Sub y for x^-1
y%5E2+%2B+8y+%2B+10+=+0
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B8x%2B10+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%288%29%5E2-4%2A1%2A10=24.

Discriminant d=24 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28-8%2B-sqrt%28+24+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%288%29%2Bsqrt%28+24+%29%29%2F2%5C1+=+-1.55051025721682
x%5B2%5D+=+%28-%288%29-sqrt%28+24+%29%29%2F2%5C1+=+-6.44948974278318

Quadratic expression 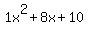1x%5E2%2B8x%2B10 can be factored:
1x%5E2%2B8x%2B10+=+%28x--1.55051025721682%29%2A%28x--6.44948974278318%29
Again, the answer is: -1.55051025721682, -6.44948974278318. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B8%2Ax%2B10+%29

----------------
The solutions shown are for y.
y = -4 ± sqrt(6)
1/x = = -4 ± sqrt(6)
---------------------
x = 1/(-4 + sqrt(6))
x = (-4 - sqrt(6))/(16 - 6)
x = (-4 ± sqrt(6))/10
=========================
Substitution is not the best method, tho.
x%5E-2+%2B+8x%5E-1+=+-10
Multiply thru by x^2
1+%2B+8x+=+-10x%5E2
10x%5E2+%2B+8x+%2B+1+=+0
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 10x%5E2%2B8x%2B1+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%288%29%5E2-4%2A10%2A1=24.

Discriminant d=24 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28-8%2B-sqrt%28+24+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%288%29%2Bsqrt%28+24+%29%29%2F2%5C10+=+-0.155051025721682
x%5B2%5D+=+%28-%288%29-sqrt%28+24+%29%29%2F2%5C10+=+-0.644948974278318

Quadratic expression 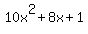10x%5E2%2B8x%2B1 can be factored:
10x%5E2%2B8x%2B1+=+%28x--0.155051025721682%29%2A%28x--0.644948974278318%29
Again, the answer is: -0.155051025721682, -0.644948974278318. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+10%2Ax%5E2%2B8%2Ax%2B1+%29

----------------
Simpler, less work, less time.