SOLUTION: x^2-5x+3 solve the equation

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: x^2-5x+3 solve the equation      Log On


   

Question 3229: x^2-5x+3 solve the equation
Answer by drglass(89) About Me  (Show Source):
You can put this solution on YOUR website!
I assmue you mean x%5E2+-+5x+%2B+3+=+0

To find a solution we will need to apply the quadratic equation, which says the roots of a quadratic equation in the form ax%5E2+%2B+bx+%2B+c+=+0are:

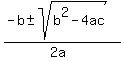
%28-b+%2B-+sqrt%28b%5E2+-+4ac%29%29%2F%282a%29
.
To use the quadratic equation we must first a, b and c, which, for this problem, are a = 1, b = -5 and c = 3. Substituting them into the quadratic, we get:


.
So there are two roots to this eqaution, x+=+%285+%2B+sqrt%2813%29%29%2F2 and x+=+%285+-+sqrt%2813%29%29%2F2. To test the correctness of this answer, substitute the roots in to the equation.

%28%285+%2B+sqrt%2813%29%29%2F2%29%5E2+-+5%28%285+%2B+sqrt%2813%29%29%2F2%29+%2B+3+=+0 and

%28%285+-+sqrt%2813%29%29%2F2%29%5E2+-+5%28%285+-+sqrt%2813%29%29%2F2%29+%2B+3+=+0

Get a calculator and check them out. Thes equations hold, therefore
x+=+%285+%2B+sqrt%2813%29%29%2F2 and x+=+%285+-+sqrt%2813%29%29%2F2 are solutions to the equation.