Question 311967: Use the discriminant to determine whether the following equations have solutions that are : 2 diff. rational solutions,2 diff. irrational solutions, exactly 1 rational solution, or 2 different imaginary solutions.
3 + 8z^2 = -7z
I am so confused, I just am not catching on to the quadratic equations
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website! Put the equation in the form  first. first.


Now comparing coefficients to the general equation,



The formula for the discriminant is,

Since 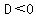 , you will have two different imaginary roots. , you will have two different imaginary roots.
.
.
Graphically, the curve never touches the x-axis, there are no real solutions.
.
.

.
.
Also, if  , you have 1 rational root, a double root. , you have 1 rational root, a double root.
If  , you have 2 distinct roots. If , you have 2 distinct roots. If  is a perfect square(1,4,9,16,...), then the two roots will be rational, if not then they will be irrational. is a perfect square(1,4,9,16,...), then the two roots will be rational, if not then they will be irrational.
|
|
|