Question 299546: This is the exact equation she gave me: "A child tosses a ball upward with an initial velocity of 10 f/s at a height of 3 feet. If it is not caught, how long will it be in the air?"
The formula she gave us to use is h(t)=-16^2+vt+s
I tried setting it equal to zero but got lost after that.
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is the exact equation she gave me: "A child tosses a ball upward with an initial velocity of 10 f/s at a height of 3 feet. If it is not caught, how long will it be in the air?"
The formula she gave us to use is h(t)=-16^2+vt+s
I tried setting it equal to zero but got lost after that.
---------------
If you set it to zero, you can find the time when it hits the ground, when h=0. That's how long it is in the air.
h(t)=-16^2+vt+s
Actually, it's h(t)=-16t^2+vt+s
h(t) = -16t^2 + 10t + 3
-16t^2 + 10t + 3 = 0
| Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc) |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=292 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 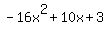 can be factored: can be factored:

Again, the answer is: -0.221500234082346, 0.846500234082346.
Here's your graph:
 |
---------------
Ignore the negative number.
t =~0.8465 seconds to impact
You were doing it right, setting it to zero.
|
|
|