Question 285401: What is the product of two consecutive numbers that is less than 10 times the smaller number?
Found 2 solutions by jsmallt9, richwmiller:
Answer by jsmallt9(3758)   (Show Source): (Show Source):
You can put this solution on YOUR website! By "consecutive numbers" I assume you mean consecutive integers. Consecutive integers are 1 apart from each other. So if one of the integers is x, then the next one is x+1. This gives us:

Simplifying we get:
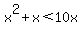
Since this is quadratic we want one side equal to zero (like a quadratic equation):

And we factor it (just like we do for an equation):
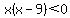
Now, because it is an inequality and not an equation, it gets a little different. We have a product that is less than zero. In other words, we have a product that is negative. And when do we get a negative result when multiplying two numbers? Answer: When one number is positive and the other number is negative.
We could now write an expression for "x is positive and x-9 is negative or x is negative and x-9 is positive":
(x > 0 and x-9 < 0) or (x < 0 and x-9 > 0)
And we could solve this. But we can make things easier with a little additional logic. We can actually figure out which factor must be the positive one and which must be the negative one, even though we do not know what x or x-9 are!
Won't x always be greater than x-9? (Think about it. After taking away 9 from x, no matter what x is, won't x-9 always be less than x?). And if x-9 is smaller than x, then won't it have to the the negative factor? (I hope this logic is obvious. If not, then just solve the compound inequality above.) With this knowledge we can just use:
x > 0 and x-9 < 0
Solving the second inequality we get:
x > 0 and x < 9
So the smaller number, x, can be any integer between 0 and 9 (not including 0 or 9).
Answer by richwmiller(17219)   (Show Source): (Show Source):
|
|
|