SOLUTION: Is it possible for a quadratic equation to have 0 solutions? 1 solution? 2 solutions? More than 2 solutions? How can you tell algebraically AND graphically how many solutions a

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: Is it possible for a quadratic equation to have 0 solutions? 1 solution? 2 solutions? More than 2 solutions? How can you tell algebraically AND graphically how many solutions a      Log On


   

Question 278943: Is it possible for a quadratic equation to have 0 solutions? 1 solution? 2 solutions? More than 2 solutions?
How can you tell algebraically AND graphically how many solutions a quadratic equation has?

Answer by richwmiller(17219) About Me  (Show Source):
You can put this solution on YOUR website!
graphically
if the parabola touches the x axis twice there are two solutions
if it touches once there is one solution
if it never touches the x axis there are no real solutions
algebraically
x^+4x+4=0
x^2-2x-3=0
x^2-2x+3=0
check out the determinants in these three equations
Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B4x%2B4+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%284%29%5E2-4%2A1%2A4=0.

Discriminant d=0 is zero! That means that there is only one solution: x+=+%28-%284%29%29%2F2%5C1.
Expression can be factored: 1x%5E2%2B4x%2B4+=+1%28x--2%29%2A%28x--2%29

Again, the answer is: -2, -2. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B4%2Ax%2B4+%29

Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B-2x%2B-3+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-2%29%5E2-4%2A1%2A-3=16.

Discriminant d=16 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--2%2B-sqrt%28+16+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-2%29%2Bsqrt%28+16+%29%29%2F2%5C1+=+3
x%5B2%5D+=+%28-%28-2%29-sqrt%28+16+%29%29%2F2%5C1+=+-1

Quadratic expression 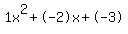1x%5E2%2B-2x%2B-3 can be factored:
1x%5E2%2B-2x%2B-3+=+1%28x-3%29%2A%28x--1%29
Again, the answer is: 3, -1. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B-2%2Ax%2B-3+%29

Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B-2x%2B3+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-2%29%5E2-4%2A1%2A3=-8.

The discriminant -8 is less than zero. That means that there are no solutions among real numbers.

If you are a student of advanced school algebra and are aware about imaginary numbers, read on.


In the field of imaginary numbers, the square root of -8 is + or - sqrt%28+8%29+=+2.82842712474619.

The solution is

Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B-2%2Ax%2B3+%29