Question 271628: How do you find the standard form, vertex, line of symmetry, and maximum or minimum values, and square the equation?
f(x)=x^2-2x-3
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! How do you find the standard form, vertex, line of symmetry, and maximum or minimum values, and square the equation?
f(x) = x^2 - 2x - 3
:
The standard form: x^2 - 2x - 3 = 0
:
Find the line of symmetry using x = -b/(2a); a=1; b= -2
x = 
x = 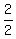
x = 1 is the line of symmetry
:
Find the vertex, substitute 1 for x in the original equation
y = 1^2 -2(1) - 3
y = 1 - 2 - 3
y = -4
The vertex: x=1, y=-4 and it is minimum (coefficient of x^2 is positive)
:
Squaring this equation (using long hand multiplication);
(x^2-2x-3)*(x^2-2x-3) = x^4 - 4x^3 - 2x^2 + 12x + 9
|
|
|