Question 262235: What are the possible number of solutions for a quadratic equation?
there are a maximum of 2 solutions since the highest order exponent is 2.
Found 2 solutions by Alan3354, Theo:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! There are always 2, but sometimes it's the same value twice.
Some would say it's either 1 or 2.
For example:
x^2 + 2x + 1 = 0
x = -1, x = -1
The 2 solutions are the same.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! if you are talking about real number solutions only, then the possible number of roots can be 0, 1, or 2.
if you are talking about real numbers or imaginary / complex numbers, then the number of solutions is 1 or 2.
an example of 1 solution would look like this:
the equation used is y = x^2.
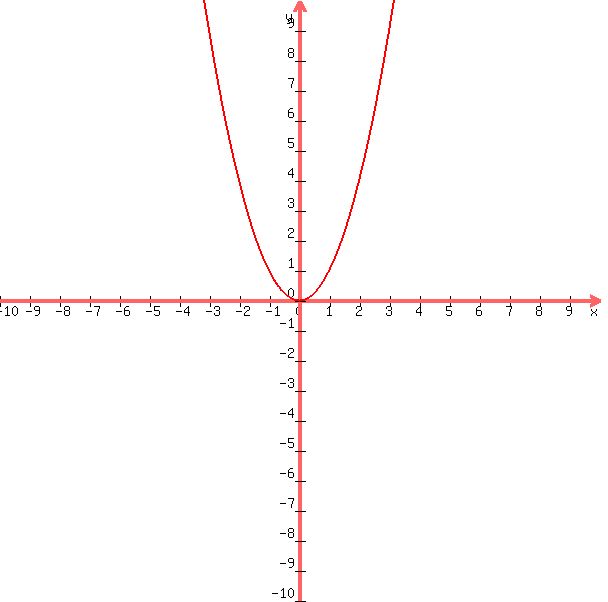
the graph only crosses the x-axis at 1 point.
an example of 2 solutions would look like this:
the equation used is y = x^2 - 5.
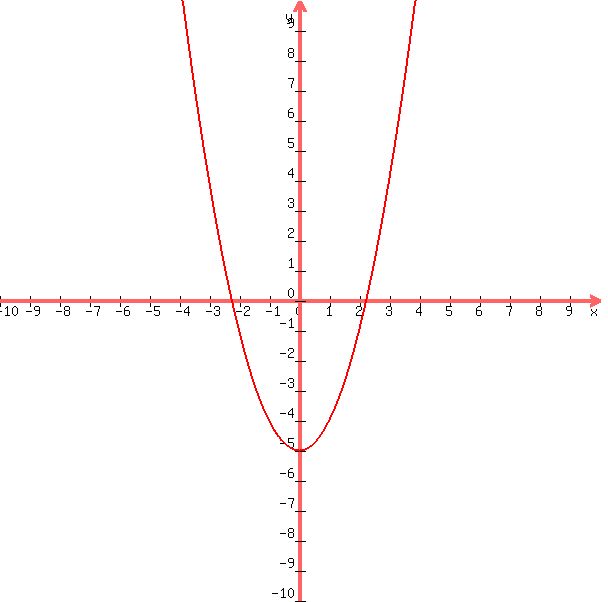
the graph crosses the x-axis at 2 points.
an example of 0 solutions would look like this:
the equation used is y = x^2 + 5.
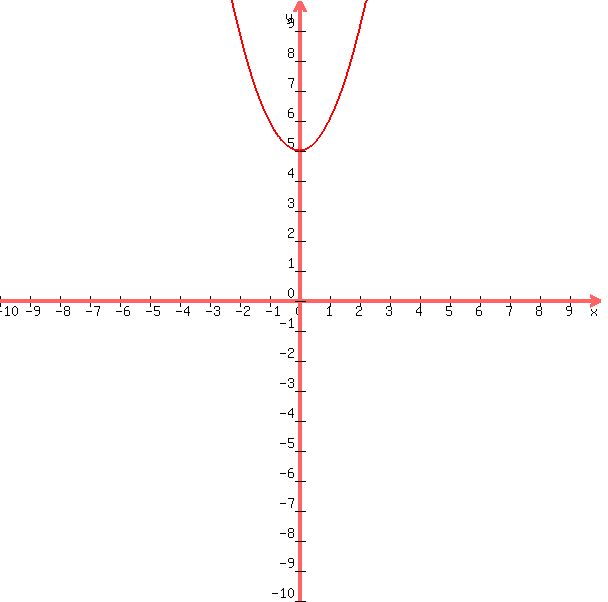
the graph does not cross the x-axis at any points.
this last graph has 0 roots if you want the roots to be only real numbers.
this last graph has 2 roots if you allow the roots to be imaginary or complex numbers only.
to solve this last problem, you would either use the completing the squares method or the quadratic formula.
I'll use the completing the squares method.
The equation is x^2 + 5 = 0
subtract 5 from both sides of the equation to get:
x^2 = -5
take the square root of both sides of the equation to get:
x = +/- sqrt(-5)
sqrt(-5) is not a real number.
since the roots imaginary, they do not count as real numbers and you say the equation has no roots as long as you require the roots to be real numbers.
as you can see, when the roots are imaginary, the graph does not cross the x-axis.
if you use the imaginary roots for the value of x in the equation, the value of the equation will be equal to 0 as required, but the requirement that the graph of the equation cross the x-axis will not have been satisfied.
for example:
when x = sqrt(-5), the value of the equation x^2 + 5 = 0 will be sqrt(-5)^2 = -5.
-5 + 5 does equal 0, so the equation is satisfied even though the graph of the equation does not cross the x-axis at those points.
bottom line:
if you define the roots as the value of x when the equation equals 0, then the imaginary values are roots.
if you define the roots as the point where the graph of the equation crosses the x-axis, then the imaginary values are not roots.
since most of the time you are dealing with real values of x only, then the answer to your question will be:
the possible number of solutions for a quadratic equation are 0, 1, or 2.
you should, however, clarify with your instructor whether he wants to include imaginary solutions as well.
in either case, the maximum number of solutions for a quadratic equation will be 2 whether or not you use only real or you include imaginary solutions as well.
|
|
|