Question 261964: Jim,
I have tried to follow and plug in the equation but it is not working. I have been at this for over an hour and my brain is fried. Help!!
Bayside Insurance offers two health plans. Under plan A Giselle would have to pay the first $140 of her bills and 25% of the rest. Under plan B she would have to pay the first $160 of her bills and 20% of the rest. For what amount of medical bills will plan B save Giselle money? Assume she has over $160 in bills.
Giselle would save with plan B if she had more than $_________in bills?
When it says assume she has over $160 in bills, does that mean you can use any number higher than 160?
Please help,
Thank you
Deborah
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! The reason why we're assuming that she has over $160 in medical bills is if she had less than $160 in bills, then she would be clearly paying more for plan B. For instance, if she has $159 in bills, then she pays almost $15 more for plan B.
Let x = amount Giselle has to pay (ie her bill)
Under plan A, she has to pay the first $140 and then 25% of the rest. So if we assume that she has over $160 in bills, this means that 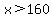 . After she pays the initial $140, then she has 25% of . After she pays the initial $140, then she has 25% of 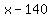 in bills left over. So this means that under plan A, the cost is in bills left over. So this means that under plan A, the cost is 
Similarly, under plan B, because "she would have to pay the first $160 of her bills and 20% of the rest", this means that the cost for plan B is 
So to figure out when plan B will save her money, simply set the plan B expression less than the plan A expression

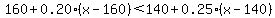 Substitute the given cost equations. Substitute the given cost equations.
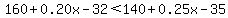 Distribute Distribute
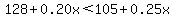 Combine like terms Combine like terms
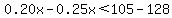 Subtract 0.25x from both sides. Subtract 128 from both sides. Subtract 0.25x from both sides. Subtract 128 from both sides.
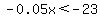 Combine like terms Combine like terms
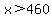 Divide both sides by -0.05. Remember that dividing both sides by a negative number will flip the inequality sign. Divide both sides by -0.05. Remember that dividing both sides by a negative number will flip the inequality sign.
So if she has any bills over $460, then Plan B will cost less than Plan A.
If you're skeptical, try some values of 'x' that are around $460. Try x=400, x=450, x=500 (and maybe more) and you'll notice that plan B will become cheaper after you pass x=450.
Note: the plans cost the same when the bill is $460. This is cross over point when the plans switch in cost.
|
|
|