SOLUTION: The vertical height, h, in metres of a golf ball as it travels a horizontal distance, d metres, down the fairway, can be described using a quadratic function. A pro-golfer can dri

Click here to see ALL problems on Quadratic Equations

Question 254211: The vertical height, h, in metres of a golf ball as it travels a horizontal distance, d metres, down the fairway, can be described using a quadratic function. A pro-golfer can drive the ball 300m down the fairway before it lands. If the ball's maximum height was 15m:
- draw a sketch of the path of the golf ball
- find the equation of the path of the golf ball
- determine the two distances down the fairway when the ball is 10m above the ground. Give your answer to the nearest tenth of a metre.
Found 2 solutions by solver91311, ankor@dixie-net.com:
Answer by solver91311(24713) (Show Source):
You can put this solution on YOUR website!

We are looking for a function

such that

and

We are given that this is a quadratic function, so:

The graph is a parabola with the vertex on the axis of symmetry, namely half-way between and , to wit: and we are given that

So from

we can deduce that in

and then

remains. Then, from

we can write:

and from

we can write:

Giving us a system of two linear equations in two variables. I recommend that you solve them by the elimination method. Once you have the coefficients for the quadratic, set the quadratic expression equal to 10 and solve for the two roots.

John

Answer by ankor@dixie-net.com(22740) (Show Source):
You can put this solution on YOUR website!
The vertical height, h, in metres of a golf ball as it travels a horizontal distance, d metres, down the fairway, can be described using a quadratic function.
A pro-golfer can drive the ball 300m down the fairway before it lands. If the ball's maximum height was 15m:
:
- draw a sketch of the path of the golf ball
- find the equation of the path of the golf ball
:
Find the equation using the form ax^2 + bx = y
Coordinate at it's highest point: 150,15
a(150^2) + 150b = 15
22500a + 150 b = 15
:
Coordinate when it strikes the ground: 300,0
a(300^2) + 300b = 0
90000a = 300b = 0
:
Multiply the 1st equation by 2, subtract the 2nd equation,
45000a + 300b = 30
90000a + 300b = 0
--------------------subtraction eliminates b, find a
-45000a = 30
a =
a = -.00067
;
Find b using the 2nd equation
90000(-.00076) + 300b = 0
-60 + 300b = 0
300b = 60
b =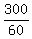
b = +.2
:
the equation of the path of the ball: h = -.00067d^2 + .2d
:
A graph of this, h = y axis; d = x axis:

:
;
determine the two distances down the fairway when the ball is 10m above the ground.
-.00067d^2 + .2d = 10
-.00067d^2 + .2d - 10 = 0
use the quadratic formula to find d:

In this problem x = d; a = -.00067, b = .2, c = -10

:

:

Two solutions

d =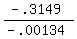
d = 235.0m
and

d =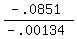
d = 63.5m
:
The ball will be a 10 meters at 63.5m and 235.0m