Question 251930: What two numbers added together equal -11 and then when the same two numbers are multiplied equal 15?
What two numbers added together equal 28 and then when those same two numbers are multiplied equal 32?
What two numbers added together equal -23 and then when those same two numbers are multiplied equal 36?
Found 2 solutions by edjones, richwmiller:
Answer by edjones(8007)   (Show Source): (Show Source):
Answer by richwmiller(17219)   (Show Source): (Show Source):
You can put this solution on YOUR website! x+y=-11
x*y=15
factors of 15
15,1
5,3
none of these add up to 11 nor have a difference of 11
x = (-11 - Sqrt[61])/2, y = (-11 + Sqrt[61])/2},
x = (-11 + Sqrt[61])/2, y = (-11 - Sqrt[61])/2}}
a+b=28
a*b=32
factors of 32
32,1
16,2
8,4
none of these add up to 28 nor have a difference of 28
a = 2(7+sqrt(41)) and b = -2(sqrt(41)-7)
a = -2 (-7 + Sqrt[41]), b = 2 (7 + Sqrt[41])
a = 2 (7 + Sqrt[41]), b = -2 (-7 + Sqrt[41])
c+d=-23
c*d=36
factors of 36
36,1
18,2
9,4
None of these add up to 23 nor have a difference of 23
c = (-23 - Sqrt[385])/2, d = (-23 + Sqrt[385])/2}
c = (-23 + Sqrt[385])/2, d = (-23 - Sqrt[385])/2}
None of these have whole numbers as factors
The graph is a line crossing a hyperbola twice
I'll go through the first one with you.
x+y=-11
x*y=15
The process be the same for the three problems
y=-11-x
x*(-11-x)=15
-11x+x^2=15
-x^2-11x=15
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=61 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 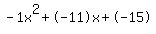 can be factored: can be factored:

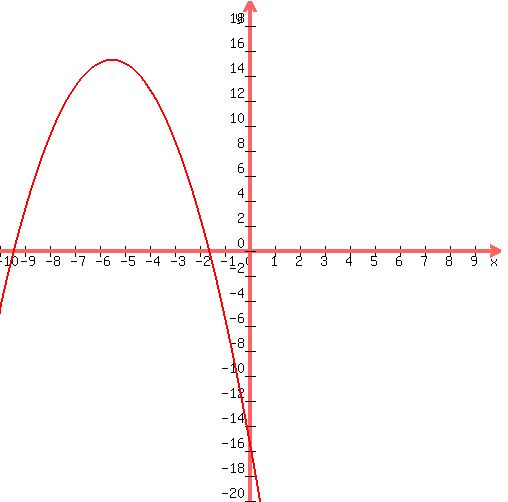
Again, the answer is: -9.40512483795333, -1.59487516204667.
Here's your graph:
 |
|
|
|