Question 249634: The length of a rectangle is 1cm more than twice the width. If the area is 78cm (squared). Find the dimensions. I came up with this so far?
L=2w +1
2w+1(w)=78
2w(squared)+w=78 then
2w(squared)+w - 78 = 0
I factored that as (2w + 13) and (2w - 6) = 0
But then I would be getting W = -13/2 and W = 6
Am I on the right track? I'm supposed to be finding the dimensions of the rectangle.
Thanks
Answer by richwmiller(17219)   (Show Source): (Show Source):
You can put this solution on YOUR website! L=2w +1
this is good
2w^2+w-78=0
divide by 2
w^2+w/2-39=0
w^2+w/2=39
[how did you get (2w + 13) and (2w - 6)
I see the 78 but where is the w?
I get 26w-12w=14w not 1w
to factor you need factors of 78 with a difference of one.
78,1
39,2
13,6
26,3
prime factors
13,3,2,1
there aren't any whole numbers]
complete the square
((1/2)(/2))^2
(1/4)^2=1/16
add 1/16 to both sides
w^2+w/2+1/16=39
(w+1/4)^2=625/16
w+1/4=+\-25/4
w=-1/4+25/4=24/4=6
w=-1/4-25/4=-26/4=-13/2
we can't use the negative solution so we have 6 for w
l=2w+1
l=13
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=625 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 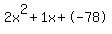 can be factored: can be factored:

Again, the answer is: 6, -6.5.
Here's your graph:
 |
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=156.25 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 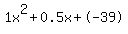 can be factored: can be factored:

Again, the answer is: 6, -6.5.
Here's your graph:
 |
|
|
|