Question 241920: if a,b are the roots of the equation 2x2+6x-10=0.Find a4+b4,a3-b3,a6+b6,a6-b6
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website! if a,b are the roots of the equation  .Find .Find  , , 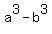 , ,  , , 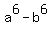
Since a, b are roots of
 they are also roots of the monic polynomial equation found
by dividing through by 2
they are also roots of the monic polynomial equation found
by dividing through by 2
 The sum of the roots is the negartive of the coefficient of x,
-3. The product of the roots is the constant number or -5
The absolute value of the difference of the roots is
The sum of the roots is the negartive of the coefficient of x,
-3. The product of the roots is the constant number or -5
The absolute value of the difference of the roots is
 If we let a be the larger root, then
If we let a be the larger root, then  So
So  , ,  , ,  So
So  So
So  So
So  Square both sides:
Square both sides:






 -------------------
-------------------
 -------------------
-------------------
 But also
But also  So
So  or or 
 But also
But also  ,
So ,
So  or or
 ------------------
------------------
 Edwin
Edwin
|
|
|