Question 23329: Can you help me with this problem and help me sketch a graph
y = x^2 + 2x -24
Thanks,
M
Answer by philberg99(10)   (Show Source):
You can put this solution on YOUR website! First of all, look at the coefficient of the  term. If it is positive, then the parabola is shaped up. If it is negative, the parabola is shaped down. The coefficient of the term is 1 so it is shaped up.
Now we have to figure out where the parabola crosses the x axis. To do this, set the equation equal to zero.
0 =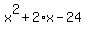 
0 = (x - 4)(x + 6)
0 = x - 4, 0 = x + 6
So x = 4, x = -6 are our solutions.
Finally, you may need to find the lowest point of this parabola, called the vertex. To find the x coordinate of the vertex, use the formula x = 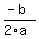 where a is the coefficient of the term and b is the coefficient of the  term. So x =  = -1. To find the y value that goes with the -1, substitute -1 in for x. That gives us y = (-1)^2 + 2(-1) - 24 = 1 - 2 - 24 = -25. So the vertex, or the lowest point of the parabola is (-1, -25).
|
|
|
