Question 216956: I am having difficulty with a question. The question is as follows: A parabola has an x-intercept at 2, its axis of symmetry is the line x=4, and the y-coordinate of its vertex is 6. Determine the equation of the parabola.
I am setting up my problem as y = ax^2 + bx + c and I since x = 4, y must be 0
o = 16 + 4 + c. I'm confused and I don't think I am setting up the equation correctly.
Thanks - Lori
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! I am having difficulty with a question.
;
The question is as follows: A parabola has an x-intercept at 2,
its axis of symmetry is the line x=4, and the y-coordinate of its vertex is 6.
Determine the equation of the parabola.
:
I am setting up my problem as y = ax^2 + bx + c and I since x = 4, y must be 0
Not right: the axis of symmetry is given as 4 and y coordinate as 6 so you have:
:
x = 4; y = 6 (vertex)
(4^2)a + 4b + c = 6
16a + 4b + c = 6
:
and the intercept
x = 2; y = 0
(2^2)a + 2b + c = 0
4a + 2b + c = 0
:
Here we can reason:
the two intercepts are equidistant from the axis of symmetry
One intercept is +2, the axis symmetry is +4 then the other intercept is +6
:
x = 6; y = 0
(6^2)a + 6b + c = 0
36a + 6b + c = 0
:
Three equations to find three unknowns, a, b, c
:
use the 1st two equations to eliminate c
16a + 4b + c = 6
4a + 2b + c = 0
-------------------Subtraction eliminates c
12a + 2b = 6
:
do the same with the 1st and 3rd equation
36a + 6b + c = 0
16a + 4b + c = 6
------------------Subtraction eliminates c
20a + 2b = -6
;
Use these two equations, and eliminate b and find a
20a + 2b = -6
12a + 2b = 6
--------------Subtraction eliminates b
8a = -12
a = 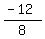
a = -1.5
:
Find b using eq: 12a + 2b = 6
12(-1.5) + 2b = 6
-18 + 2b = 6
2b = 6 + 18
2b = 24
b = 12
:
Find c using eq: 4a + 2b + c = 0
4(-1.5) + 2(12) + c = 0
-6 + 24 + c = 0
18 + c = 0
c = -18
:
The equation: y = -1.5x^2 + 12x -18
:
Check this by graphing it

Two x intercepts at +2 and +6; vertex: 4,6.
|
|
|