SOLUTION: Trains a and b are traveling in the same direction on parallel tracks. Train A is traveling at 80mph...? B is at 88mpr. Train A passes a station at 8:20pm. If train B passes the sa

You can do it in your head:

When train B passes the station at 8:50pm, train
A has been travelingfor half an hour at 80mph 
(since 8:20pm) and so it is 40 miles from train B.
So A's approach rate is 88-80 or 8mph and so it 
will take 5 hours to shrink A's 40 mile head start 
down to zero. So 5 hours from 8:50pm is 1:50am.
(That is, provided the train did not cross over 
a time zone!)  

  
But your teacher doesn't want you to do it that way.  That's too easy
and you don't learn any algebra:

Let t = the time train B travels till it catches A.

Make this chart:

Train    Distance   Rate   Time
  A 
  B

Then fill 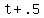in  for the time of train A,
since it traveled for half an hour (or .5 hours)
past the station when B left the station.

Also fill in their rates of 80mph and 88mph

Train    Distance   Rate   Time
  A                  80    t+.5  
  B                  88     t

Now we use  Distance = Rate x Time to fill in
the distances both will have traveled from the station.

Train    Distance   Rate   Time
  A       80(t+.5)   80    t+.5  
  B         88t      88     t

When B catches up to A they will have traveled the
same distance so we set those two distances equal:

A's distance from station = B's distance from station  

             90(t+.5) = 88t

Solve that and get t=5 hours

Then 5 hourslater than 8:50pm is 1:50am, provided no 
time zone was crossed.

Edwin