Question 206491This question is from textbook Elementary and Intermediate
: 3x2(squared)+48=24X
This question is from textbook Elementary and Intermediate
Answer by mickclns(59)   (Show Source): (Show Source):
You can put this solution on YOUR website!  divide both sides, then subtract 8x from both sides divide both sides, then subtract 8x from both sides
 factor or use quadratic formula or use special factoring factor or use quadratic formula or use special factoring
Factor
There are various ways of factoring a quadratic (if it factors, which this does). I like this way: First multiply the coefficient of the  term, 1, by the constant term, 16, to get 16. Now you want to find two numbers that multiply to this number, 16, and that add to the coefficient of x, in this case -8. The two numbers are -4 and -4. term, 1, by the constant term, 16, to get 16. Now you want to find two numbers that multiply to this number, 16, and that add to the coefficient of x, in this case -8. The two numbers are -4 and -4.
Now you put those two numbers into the blanks in 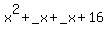 : :
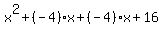
Now factor out whatever you can out of the first two terms and factor out whatever you can out of the last two terms:
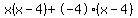 Notice both terms have a factor of x-4 which you can factor out: Notice both terms have a factor of x-4 which you can factor out:
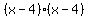 or or 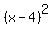
Now we use the zero product property which says that if a product of a bunch of numbers is 0 then one of the numbers must be 0, which is what allows us to set each of the factors to 0 (and which is why we subtracted 8x from each side above).
So,  --> (since 0 is the only number whose square is 0), x-4 = 0 --> x=4 --> (since 0 is the only number whose square is 0), x-4 = 0 --> x=4
To check the answer, plug 4 in for x in the ORIGINAL equation and simplify
Is  ? ?
 ? ?
 ? ?
 Yes! Yes!
Quadratic Formula:
(sorry if you read the solution that had an error, I accidentally pressed the button that indicated I was finished)
 --> --> 
 a = 1, b=-8, c = 16 (notice you can only use this when one side is 0) a = 1, b=-8, c = 16 (notice you can only use this when one side is 0)




Special Factoring
For any a and b (a and b can be any expression, not just numbers!),  the two (+or- )'s are always the same and the squares are positive the two (+or- )'s are always the same and the squares are positive
Notice In this case,
 , in the first term a = x, in the third term b = -4 (why - instead of +?), so the question is: in the middle term, do we have 2ab? 2ab = 2(x)(-4) = -8x, so the answer is Yes" , in the first term a = x, in the third term b = -4 (why - instead of +?), so the question is: in the middle term, do we have 2ab? 2ab = 2(x)(-4) = -8x, so the answer is Yes"
So,  and we have the same equation as in the first section: and we have the same equation as in the first section: 
|
|
|