Question 205543: Please help me solve
Bayside Insurance offers two health plans. Under Plan A, Sam would have to pay the first $170 of his medical bills, plus 35% of the rest. Under Plan B, Sam would pay the first $210, but only 30% of the rest. For what amount of medical bills will Plan B save Sam money? Assume he was over $210 in bills. Sam would save with Plan B if he had more than $_____ in bills.
Found 2 solutions by Theo, stanbon:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! problem:
Bayside Insurance offers two health plans. Under Plan A, Sam would have to pay the first $170 of his medical bills, plus 35% of the rest. Under Plan B, Sam would pay the first $210, but only 30% of the rest. For what amount of medical bills will Plan B save Sam money? Assume he was over $210 in bills. Sam would save with Plan B if he had more than $_____ in bills.
-----
let x = cost of sam's medical bills.
-----
Under Plan A, Sam pays 170 + .35 * (x - 170)
Under Plan B, Sam pays $210 + .3 * (x - 210)
-----
Assume x > $210
-----
Break even point is when Plan A costs the same as plan B.
This happens when:
170 + .35*(x-170) = 210 + .3*(x-210)
-----
removing the parentheses, this equation becomes:
170 + .35x - 59.5 = 210 + .3x - 63
simplifying, this becomes:
110.5 + .35x = 147 + .3x
subtracting 110.5 from both sides and subtracting .3x from both sides of the equation gets:
.35x - .3x = 147 - 110.5
simplifying gets:
.05x = 36.5
dividing both sides of the equation by .05 gets:
x = 730
-----
testing by substituting in the break even equation gets:
170 + .35*(730-170) = 210 + .3*(730-210)
removing parentheses gets:
170 + 255.5 - 59.5 = 210 + 219 - 63
simplifying gets:
366 = 366
confirming that the value of x is good.
-----
Answer to your question is:
Sam would save with plan B is Sam had more than $730 in bills.
-----
As a test, assume Sam has $750 in bills.
Under plan A Sam would pay:
170 + .35*(750 - 170) = 170 + .35 * (580) = 170 + $203 = $373
Under plan B Sam would pay:
210 + .3*(750-210) = 210 + .3 * (540) = 210 + 162 = $372
-----
The numbers might be smaller but you could test with as little as a penny over the break even point.
To make it reasonable, we'll use $1.00 over the break even point.
Assume the bills were $731.
Under Plan A Sam would pay $170 + (.35)*($731-$170) = $170 + .35*561 = $366.35
Under Plan B Sam would pay $210 + (.3)*($731-$210) = $210 + .34*521 = $366.30
-----
A graph of both equations would show this.
Below $730 Plan A should be cheaper.
Above $730 Plan B should be cheaper.
-----
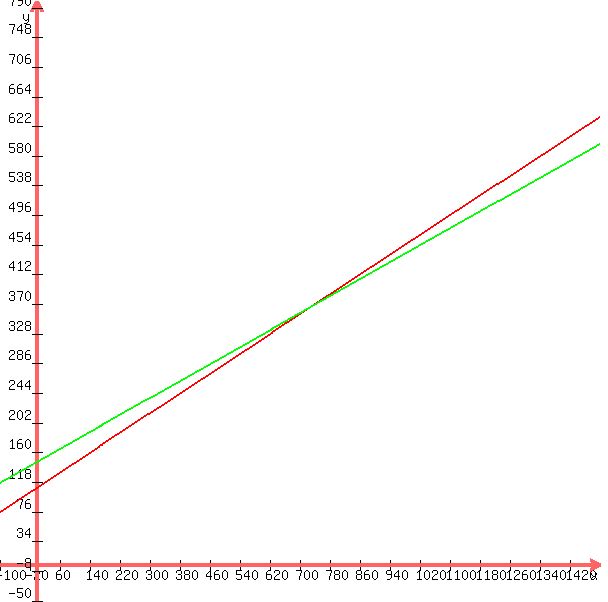
-----
when x = 0, plan A intersects the y axis at 110.5
when x = 0, plan B intersect the y axis at 147.00
-----
you can see that plan A is cheaper than plan B up to x = $731 and then becomes more expensive.
-----
You could have worked this directly by making the plan b equation less than the plan a equation rather than equal.
-----
if you did that you would have had:
210 + .3*(x - 210) < 170 + .35*(x - 170)
you solve in the same way but you're dealing with an inequality now and the inequality rules prevail.
first thing is to remove the parentheses.
equation becomes:
210 + .3x - (.3*210) < 170 + .35x - (.35*170)
subtracting 170 from both sides and subtracting .3x from both sides and adding (.35*170) to both sides gets:
210 - 170 - (.3*210) + (.35*170) < .35x - .3x
combining like terms gets:
40 - (.3*210) + (.35*170) < .05x
simplifying further gets:
40 - 63 + 59.5 < .05x
which becomes:
36.5 < .05x
dividing both sides by .05 gets:
36.5/.05 < x
which becomes:
730 < x
-----
730 < x is the same as x > 730 so the result of this equation is x > 730.
when x is greater than 730 plan b is cheaper.
-----
this is the same result we got earlier so it confirms the results and was more direct because the inequality equation rather than the break even equation was used.
-----
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! Bayside Insurance offers two health plans.
Under Plan A, Sam would have to pay the first $170 of his medical bills, plus 35% of the rest.
Under Plan B, Sam would pay the first $210, but only 30% of the rest.
-----------------------
For what amount of medical bills will Plan B save Sam money?
Let the medical bills be "x" dollars:
Plan A cost: 170+ 0.35(x-170)
Plan B cost: 210+ 0.30(x-210)
---
Inequality:
Plan B < Plan A
210 + 0.30(x-210) < 170 + 0.35(x-170)
0.70*210 + 0.30x < 0.65*170 + 0.35x
0.05x > 36.6
x > $730
----------------------------------------------------
Assume he was over $210 in bills. Sam would save with Plan B if he had more than $_730.00____ in bills.
============================================
Cheers,
Stan H.
|
|
|