SOLUTION: I am very confused by algebra and need help, can someone help me with this word problem? A rectangular garden has dimensions of 15f by 11f. A gravel path of uniform width is to be

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: I am very confused by algebra and need help, can someone help me with this word problem? A rectangular garden has dimensions of 15f by 11f. A gravel path of uniform width is to be      Log On


   

Question 204074: I am very confused by algebra and need help, can someone help me with this word problem?
A rectangular garden has dimensions of 15f by 11f. A gravel path of uniform width is to be built around the garden. How wide can the path be if there is enough gravel for 192 sq.ft ?
Found 2 solutions by Earlsdon, jojo14344:
Answer by Earlsdon(6294) About Me  (Show Source):
You can put this solution on YOUR website!
It's probably a good idea to draw yourself a diagram of this situation.
Draw a larger rectangle to represent the garden with the gravel path in place, then inside of that rectangle, draw a smaller similar rectangle to represent the 11ft. by 15ft. garden.
Let the width of the gravel path be x ft.
You need to write the area of the gravel path in terms of x, its width.
Think...write an expression for the whole thing, garden plus gravel path, then subtract the area of the garden alone. This will give you an expression for the area of the gravel path.
Step 1. Area of the whole thing:
A+=+L%2AW
The length of the whole thing can be expressed as L = 15+2x
The width can be expressed as W = 11+2x
The area is:
A%5Bw%5D+=+%2815%2B2x%29%2811%2B2x%29 Use the FOIL method to multiply.
A%5Bw%5D+=+165%2B52x%2B4x%5E2 or highlight%28A%5Bw%5D+=+4x%5E2%2B52x%2B165%29 Now we subtract the area of the garden alone and this is:
Step 2. Area of the gravel path.
A%5Bg%5D+=+L%2AW Substitute L = 15 and W = 11
A%5Bg%5D+=+%2815%29%2A%2811%29
highlight_green%28A%5Bg%5D+=+165%29
So the area of the gravel path alone is:
A%5Bp%5D+=+highlight%28A%5Bw%5D%29-highlight_green%28A%5Bg%5D%29 or:
A%5Bp%5D+=+highlight%284x%5E2%2B52x%2B165%29-highlight_green%28165%29 and this is equal to 192 sq.ft., so...
4x%5E2%2B52x+=+192 Subtract 192 from both sides.
4x%5E2%2B52x-192+=+0 Factor out a 4 to simplify the calculations a bit.
4%28x%5E2%2B13x%2B48%29+=+0 so we can write:
x%5E2%2B13x%2B48+=+0 Factor this trinomial.
%28x%2B16%29%28x-3%29+=+0 Apply the zero product rule:
x%2B16+=+0 or x-3+=+0 which means that...
cross%28x+=+-16%29 or x+=+3 Discard the negative solution as the width of the gravel path must be a positive value.
The width of the gravel path is 3 feet.

Answer by jojo14344(1513) About Me  (Show Source):
You can put this solution on YOUR website!


The problem states the gravel is enough for 192 sq. ft. ---> uniform width built around the garden.

Let us see the garden then,


As you can see, we need to SUBTACT 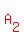red%28A%5B2%5D%29 to green%28A%5B1%5D%29 for us to get 192 sq. ft of gravel used for the uniform width.

It follows,
red%28A%5B2%5D%29-green%28A%5B1%5D%29=192ft%5E2
%2815%2Bx%2Bx%29%2811%2Bx%2Bx%29-%2815%29%2811%29=192ft%5E2
%2815%2B2x%29%2811%2B2x%29-%2815%29%2811%29=192
cross%28165%29%2B22x%2B30x%2B4x%5E2-cross%28165%29=192
4x%5E2%2B52x-192=0, wheresystem%28a=4%2Cb=52%2Cc=-192%29

By Quadratic Eqn,
Solving discriminant, b%5E2-4ac=52%5E2-4%284%29%28-192%29=2704%2B3072=red%285776%29
Then,
x=+%28-52%2B-sqrt%285776%29%29%2F%282%2A4%29=%28-52%2B-76%29%2F8
x=%28-52-76%29%2F8=-128%2F8=-16%29,disregard (-)
x=%28-52%2B76%29%2F8=24%2F8
highlight%28red%28x=3ft%29%29, (Answer) ---> the uniform width

Let us check,
red%28A%5B2%5D%29-green%28A%5B1%5D%29=192ft%5E2

%2821%29%2817%29-%2815%29%2811%29=192
357-165=192
192ft%5E2=192ft%5E2

Thank you,
Jojo