SOLUTION: Solve by completing the square: x^2+6x-5=0

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: Solve by completing the square: x^2+6x-5=0      Log On


   

Question 202156: Solve by completing the square: x^2+6x-5=0
Answer by vleith(2983) About Me  (Show Source):
You can put this solution on YOUR website!
x%5E2%2B6x-5=0
x%5E2%2B6x+=+5
x%5E2+%2B6x+%2B9+=+5+%2B+9
%28x%2B3%29%5E2+=+14
x%2B3+=+sqrt%2814%29
x+=+-3%2Bsqrt%2814%29 or x=-3-sqrt%2814%29
x=0.741 or x=-6.741
Here are more words - same thing
Solved by pluggable solver: COMPLETING THE SQUARE solver for quadratics
Read this lesson on completing the square by prince_abubu, if you do not know how to complete the square.
Let's convert 1x%5E2%2B6x%2B-5=0 to standard form by dividing both sides by 1:
We have: 1x%5E2%2B6x%2B-5=0. What we want to do now is to change this equation to a complete square %28x%2Bsomenumber%29%5E2+%2B+othernumber. How can we find out values of somenumber and othernumber that would make it work?
Look at %28x%2Bsomenumber%29%5E2: %28x%2Bsomenumber%29%5E2+=+x%5E2%2B2%2Asomenumber%2Ax+%2B+somenumber%5E2. Since the coefficient in our equation 1x%5E2%2Bhighlight_red%28+6%29+%2A+x%2B-5=0 that goes in front of x is 6, we know that 6=2*somenumber, or somenumber+=+6%2F2. So, we know that our equation can be rewritten as %28x%2B6%2F2%29%5E2+%2B+othernumber, and we do not yet know the other number.
We are almost there. Finding the other number is simply a matter of not making too many mistakes. We need to find 'other number' such that %28x%2B6%2F2%29%5E2+%2B+othernumber is equivalent to our original equation 1x%5E2%2B6x%2Bhighlight_green%28+-5+%29=0.


The highlighted red part must be equal to -5 (highlighted green part).

6%5E2%2F4+%2B+othernumber+=+-5, or othernumber+=+-5-6%5E2%2F4+=+-14.
So, the equation converts to %28x%2B6%2F2%29%5E2+%2B+-14+=+0, or %28x%2B6%2F2%29%5E2+=+14.

Our equation converted to a square 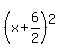%28x%2B6%2F2%29%5E2, equated to a number (14).

Since the right part 14 is greater than zero, there are two solutions:

system%28+%28x%2B6%2F2%29+=+%2Bsqrt%28+14+%29%2C+%28x%2B6%2F2%29+=+-sqrt%28+14+%29+%29
, or

system%28+%28x%2B6%2F2%29+=+3.74165738677394%2C+%28x%2B6%2F2%29+=+-3.74165738677394+%29
system%28+x%2B6%2F2+=+3.74165738677394%2C+x%2B6%2F2+=+-3.74165738677394+%29
system%28+x+=+3.74165738677394-6%2F2%2C+x+=+-3.74165738677394-6%2F2+%29

system%28+x+=+0.741657386773941%2C+x+=+-6.74165738677394+%29
Answer: x=0.741657386773941, -6.74165738677394.