Question 199563: 3. Steve traveled 150 miles at a certain speed. Had he gone 20mph faster, the trip would have taken 2 hours less. Find the speed of his vehicle.
i think it is 30mph but I cannot figure out the equation
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Remember, the distance-rate-time formula is

Since he "traveled 150 miles at a certain speed", this means that the first equation is  (simply plug in d=150) (simply plug in d=150)
The statement "Had gone 20mph faster, the trip would have taken 2 hour less", tells us that the next equation is  (the distance is the same, but the speed is now 20 mph faster and the time is 2 hours shorter) (the distance is the same, but the speed is now 20 mph faster and the time is 2 hours shorter)
The goal is to use this system to solve for "r" (and if we want, "t" also)
 Start with the first equation. Start with the first equation.
 Divide both sides by r. Divide both sides by r.
 Rearrange the equation Rearrange the equation
 Move onto the second equation. Move onto the second equation.
 Plug in Plug in 
 FOIL FOIL
 Multiply EVERY term by the LCD Multiply EVERY term by the LCD  to clear out the fraction. to clear out the fraction.
 Subtract Subtract 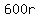 from both sides. from both sides.
 Combine and rearrange the terms. Combine and rearrange the terms.
Notice we have a quadratic in the form of 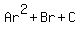 where where  , ,  , and , and 
Let's use the quadratic formula to solve for "r":
 Start with the quadratic formula Start with the quadratic formula
 Plug in Plug in  , ,  , and , and 
 Negate Negate  to get to get  . .
 Square Square  to get to get  . .
 Multiply Multiply 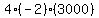 to get to get 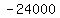
 Rewrite Rewrite 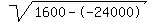 as as 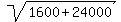
 Add Add  to to 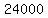 to get to get 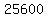
 Multiply Multiply  and and  to get to get  . .
 Take the square root of Take the square root of 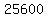 to get to get  . .
 or or  Break up the expression. Break up the expression.
 or or  Combine like terms. Combine like terms.
 or or  Simplify. Simplify.
So the possible solutions are  or or 
Since a negative speed doesn't make any sense, this means that we must ignore 
====================================================================
Answer:
So the only solution is  which means that he was traveling 30 mph. So you are correct, good job. which means that he was traveling 30 mph. So you are correct, good job.
|
|
|