SOLUTION: Hello, I have to provide a real life example of quadratic function. I have no idea where to start. Can you help me with some ideas and formulas for the everyday use of quadratic fu

A rectangular field adjacent to the straight bank of a river is to 
be fenced, but there is to be no fencing along the riverbank. If 180 m 
of fencing is available, what is the maximum area that can be 
enclosed?

We draw a rectangle for the area, with a dotted line
for the river bank:

 

If we let x ft. be the length of the left and right sides,
the bottom side will be 200 ft - 2x ft.  So we put x on
the two vertical sides and 200-2x on the horizontal side.



Let y = the area of the rectangle.

Use , so we have







  (Note: this is a quadratic equation)

If we draw the graph of that we get:


   
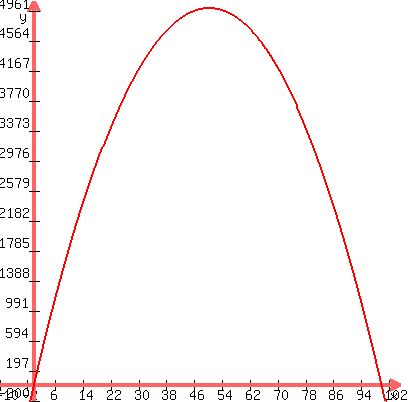Since the graph is symmetrical, the highest point
is right in the middle between the two x-intercepts.

So we find the two x-intercepts by setting y=0 and
solving for x:





Factor the left side:



,  
,   

Halfway between those will be
where x = 50

So the two vertical sides will be 50 feet each,
and the base will be 200 - 2x or



or 100 feet.  And that maximum area will be

(base)(height) = (100)(50) = 5000 square feet.

Edwin