Question 18584: If you have a string of length 50 cm, what are the dimensions of the rectangle of maximum area that you can enclose with your string? Explain your reasoning. What about a string of length k cm?
I've gotten up to the quadratic equation for the area, which is X^2 - 25X = Area. Then you have to find the third component of the formula which I don't know how to do. Then you have to state what x and y are, and I don't really know that, either. This is finding a formula, and without information on x and y, I don't see how you can actually find the numbers.
The last part of question asks for a general formula, and the book says it's
k/4 by k/4. So, I have the answer, but no explanation, which is the most important part. This doesn't make sense unless the rectangle is a square, because with a rectangle the two k's would be different. Can you help me with this?
Thank you in advance.
-Jessie
Answer by Earlsdon(6294)   (Show Source): (Show Source):
You can put this solution on YOUR website! Ok, you can let x = the length of one side of the rectangle and y = the length of the other side of the rectangle.
The area is:

and the perimeter is:
 Solve this in terms of y. Divide both sides by 2. Solve this in terms of y. Divide both sides by 2.
 Subtract x from both sides. Subtract x from both sides.
 Now substitute this into the equation for the area. Now substitute this into the equation for the area.
 Simplify. Simplify.
 What you have here is a quadratic equation whose graph is a parabola that opens downward. If you were to graph this, you would be graphing a function like: What you have here is a quadratic equation whose graph is a parabola that opens downward. If you were to graph this, you would be graphing a function like:  and you can see that y in this function plays the role of A, the area. and you can see that y in this function plays the role of A, the area.
You want to find the value of x that would make A (or y) a maximum.
You could do this using differential calculus but there is a way to do it with algebra.
Since the graph of the quadratic is a parabola opening downward, the vertex of the parabola would be at the maximum point on the curve, right? The x-coordinate, which represents the length of the side of your rectangle, is given by:
 and this is taken from the general form of quadratic equation: and this is taken from the general form of quadratic equation: 
In your quadratic equation: 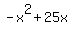 , a = -1, b = 25, and c = 0 , a = -1, b = 25, and c = 0
so we can find the x-coordinate of the vertex by:
So the length (x) of the rectangle must be 12.5 cm to get the maximum area.
But what about the width (y)?
Since the perimeter is 50 cm and this is twice the (length + width), the (length + width) is 25 cm, so the width is 25 cm - the length.




So, we end up with x (the length) = 12.5 cm and y (the width) = 12.5 cm.
And this, of course, is a square whose sides are 12.5 cm
If the perimeter were k cm, then you would use the same technique and your quadratic equation would look like:
 and the x-coordinate of the vertex of the parabola would be: and the x-coordinate of the vertex of the parabola would be:


The sides of the rectangle then would be:
 and and 
|
|
|