Question 1830: i need help completing the square for the equation: x2+6x-7=0! please :) thanks
Found 2 solutions by Ne0, longjonsilver:
Answer by Ne0(6)   (Show Source): (Show Source):
You can put this solution on YOUR website! I am new to tutoring here so I am not quite familiar with all the resources on this site yet but I'll give it a shot.
When you type x2 I assume you mean x^2.
We will start by adding the seven to both sides of your equation. Your equation should look like this: x^2+6x=7.
Now you have to check and make sure that your coefficient in front of your x^2 term is one. The reason behind this is that it makes completing the square a lot easier on us later on.
The next step is to take the middle term 6x and (ignoring the x term) divide it by 2 so you get 6/2=3. You will then take the 3 and square it which gives you 3^2=9.
What we want to do now is add this new value of 9 to both sides of the equation which results in x^2+6x+9=7+9. The reason behind adding 9 to both sides is that what you do on one side of the equation requires you to do so on the other side in order to not alter the equation. We now have a perfect square on the left side which we can factor into identical terms. After factoring we get (x+3)(x+3)=16. Since the terms are identical we can combine them like so:  . .
By simply subtracting 16 from both sides we have completed the square for the equation and our final answer is:  . I hope this helps you understand now the approach on completing the square. . I hope this helps you understand now the approach on completing the square.
Answer by longjonsilver(2297)   (Show Source): (Show Source):
You can put this solution on YOUR website! completing the square...we want the form 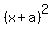 or or 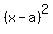 . These will give expanded polynomials like... . These will give expanded polynomials like...
 --1 --1
 --2 --2
so, your polynomial is  . Ignore the c value (-7 in this case), we are interested in the first two terms. . Ignore the c value (-7 in this case), we are interested in the first two terms.
IF, i repeat IF we have 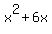 then what would be the final number, c? THAT is the question you need to answer, so lets look at equation 1 above and ours and compare them... then what would be the final number, c? THAT is the question you need to answer, so lets look at equation 1 above and ours and compare them...
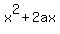
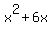
as you can see, the 2a=6 therefore a must be 3. Now if a is 3 then the  term will be 9. So basically, we NEED to have term will be 9. So basically, we NEED to have 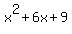
However we have -7 and not 9, so look at the equation below and convince yourself that it is the same polynomial as your original one...
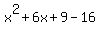
Effectively all i have done is split the -7 into 2 numbers which still add up to give -7, so there is no change in the polynomial. However, I can now use the 9 to re-write the polynomial, as


 = +4 or -4 = +4 or -4
hence x=-7, x=+1
cheers
Jon.
|
|
|