Question 177806: Quadratic Relations
A basketball shot is taken from a horizontal distance of 5m from the hoop. The height of the ball can be modelled by the relation h=-7.3t^2+8.25t+2.1, where h is the height, in metres, and t is the time, in seconds, since the ball was released.
a) From what height was the ball released?
b) What was the maximum height reached by the ball?
c) If the ball reached the hoop in 1 s, what was the height of the hoop?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A basketball shot is taken from a horizontal distance of 5m from the hoop. The height of the ball can be modelled by the relation h=-7.3t^2+8.25t+2.1, where h is the height, in metres, and t is the time, in seconds, since the ball was released.
:
a) From what height was the ball released?
Released when t = 0, therefore -7.3(0^2) + 8.25(0) + 2.1 = 2.1 meters
:
b) What was the maximum height reached by the ball?
Max height occurs at the axis of symmetry, x = -b/(2a; in this equation we have:
t = 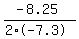
t = .565 sec
Max height = -7.3(.565^2) + 8.25(.565) + 2.1,
h = -2.33 + 4.66 + 2.1
h = 4.43 meters max height
:
c) If the ball reached the hoop in 1 s, what was the height of the hoop?
Substitute 1 for t, find h
h =-7.3(1^2) + 8.25(1) + 2.1
h =-7.3 + 8.25 + 2.1
h = 3.05 meters
|
|
|