Question 17561: How do you write in the form of y=a(x-p)2+q from y=x2-6x+10?
Answer by rapaljer(4671)   (Show Source):
You can put this solution on YOUR website! Use the process called "completing the square". Given:
 you need to write this in the form 
You do this by taking the coefficient of x, which is -6, and take half of it, and square, which is +9. The trick is to add +9 and subtract 9 on the right side, in order to do what needs to be done, but keep the equation the same.
Notice that the quantity 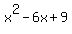 is a perfect square trinomial, and  .
So, write:
That should do it! In your formula, a=1, p=3 and q = 1. Right??
Also, the vertex is at x=3 and y = 1, which is (p,q) = (3,1)!
Is (3.1) the vertex of this parabola???
R^2 at SCC
|
|
|
