Question 175333: make a quadratic equation with the maximum value 10 and the x intercepts 1 and 3
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! make a quadratic equation with the maximum value 10 and the x intercepts 1 and 3
:
we know that the max value of y is on the axis of symmetry which is half-way
between the intercepts so max (vertex) is a x=2; y=10
;
we have three coordinates of this equation:
x=1, y=0
x=2, y=10
x=3, y=0
:
Using the form ax^2 + bx + c = y, we can solve for a, b, c
;
x=1,y=0
eq1: a + b + c = 0
:
x=2,y=10
eq2: 4a + 2b + c = 10
:
x=3,y=0
eq3: 9a + 3b + c = 0
:
Using equations 2 and 1, eliminate c
4a + 2b + c = 10
a + b + c = 0
-------------------subtraction eliminates c
3a + b = 10
:
Using equations 2 and 3, eliminate c again
4a + 2b + c = 10
9a + 3b = c = 0
---------------------subtract
-5a - b = 10
:
Add these two a&b equations
3a + b = 10
-5a- b = 10
----------------additions eliminates b
-2a = 20
a = 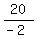
a = -10
:
Find b using equation 3a + b = 10, substitute -10 for a
3(-10) + b = 10
-30 + b = 10
b = 40
:
Find c using eq1:
-10 + 40 + c = 0
30 + c = 0
c = -30
:
Our equation: y = -10x^2 + 40x - 30
;
Looks like this:

|
|
|