Question 174303: How many solutions does the polynomial have?
How many real solution(s) does the polynomial have?
Find all zeros of the polynomial?
f(x)= x^3+x^2+2x+24
**When i did this myself for the first question i put one and for the second question i put one and for the last question my answer was x= 2,-4,-3 but im not sure if it is right.**
Answer by vleith(2983)   (Show Source):
You can put this solution on YOUR website! Since the polynomial has a degree of 3 (x^3), it has three solutions. If you have to 'do it by hand', you can always find the 'possible' real answers by looking at the factors of the coefficients that make up the high order term and the lowest order term. Since the high order temr is one, the possible real answers will be +_
1,2,3,4,6,8,12,24 . Then you just use trial and error to find that -3 works
Use this URL first --> http://www.hostsrv.com/webmab/app1/MSP/quickmath/02/pageGenerate?site=quickmath&s1=algebra&s2=factor&s3=basic
From that answer 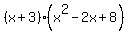 you see there is one real answer 
Then use the quadratic equation to find the other two
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case  ) has the following solutons:
For these solutions to exist, the discriminant  should not be a negative number.
First, we need to compute the discriminant :  .
The discriminant -28 is less than zero. That means that there are no solutions among real numbers.
If you are a student of advanced school algebra and are aware about imaginary numbers, read on.
In the field of imaginary numbers, the square root of -28 is + or -  .
The solution is 
Here's your graph:
 |
|
|
|
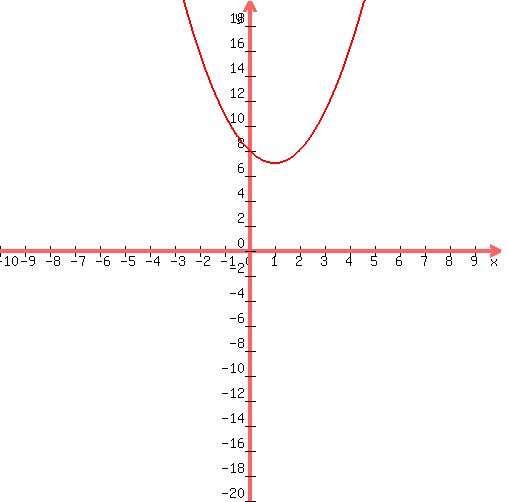