Question 172956: I have been trying this problem and I am stuck and need help! my final is monday.
One positive integer is 7 less than twice another. The sum of their squares is 202. What are the integers? Define a variable. Set up a quadratic equation. Solve, show all your work.
If you could show me all the work too that would be great so I can know how to do it next time.
Thank you
Found 2 solutions by Alan3354, stanbon:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! One positive integer is 7 less than twice another. The sum of their squares is 202. What are the integers? Define a variable. Set up a quadratic equation. Solve, show all your work.
----------------
Call them x and y. (variables defined, 2 of them)
y + 7 = 2x --> y = 2x - 7
x^2 + y^2 = 202
Sub for y
(2x-7)^2 + x^2 = 202
4x^2 -28x + 49 + x^2 = 202
5x^2 - 28x - 153 = 0 (Quadratic equation)
| Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc) |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=3844 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 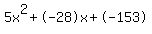 can be factored: can be factored:

Again, the answer is: 9, -3.4.
Here's your graph:
 |
------------
-3.4 is not a positive integer, so discard it.
Also, the onsite solver gets the factors wrong when the coeff of the x^2 term is not 1, so take that into account.
---------------
x = 9
y = 11
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! One positive integer is 7 less than twice another. The sum of their squares is 202. What are the integers? Define a variable. Set up a quadratic equation.
----------------
Equations:
Let one interger be "x".
Then the other is "2x-7".
-------------------------
x^2 + (2x-7)^2 = 202
x^2 + 4x^2 - 28x + 49 = 202
5x^2 -28x - 153 = 0
x = [28 +- sqrt(28^2 - 4*5*-153)]/10
x = [28 +- sqrt(3844)]/10
x = [28 +-62]/10
x = [28+62]/10 or x = [28-62]/10
Positive solution:
x = 9 (1st integer)
x-7 = 2 (2nd integer)
==================================
Cheers,
Stan H.
|
|
|