SOLUTION: 1. Determine whether the following equations have a solution or not? Justify your answer. a) x2 + 6x - 7 = 0 b) z2 + z + 1 = 0 c) (3)1/2y2 - 4y - 7(3)1/2 = 0 d) 2x2 - 10x +

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: 1. Determine whether the following equations have a solution or not? Justify your answer. a) x2 + 6x - 7 = 0 b) z2 + z + 1 = 0 c) (3)1/2y2 - 4y - 7(3)1/2 = 0 d) 2x2 - 10x +      Log On


   

Question 172100: 1. Determine whether the following equations have a solution or not? Justify your answer.
a) x2 + 6x - 7 = 0
b) z2 + z + 1 = 0
c) (3)1/2y2 - 4y - 7(3)1/2 = 0
d) 2x2 - 10x + 25 = 0
e) 2x2 - 6x + 5 = 0
f) s2 - 4s + 4 = 0
g) 5/6x2 - 7x - 6/5 = 0
h) 7a2 + 8a + 2 = 0
2. If x = 1 and x = -8, then form a quadratic equation.
3. What type of solution do you get for quadratic equations where D < 0? Give reasons for your answer. Also provide an example of such a quadratic equation and find the solution of the equation.
4. Create a real-life situation that fits into the equation (x + 4)(x - 7) = 0 and express the situation as the same equation.

Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
1. In the first place, ALL quadratic equations have two roots -- The Fundamental Theorem of Algebra says so. The question is, are the roots real numbers or not. Use the discriminant to make the determination.

The discriminant is the part of the quadratic formula that is under the radical sign.

Quadratic formula: x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+

So the discriminant is: DELTA+=+b%5E2-4ac

Use the discriminant to determine the character of the roots of a quadratic equation.

if DELTA=0 there is one real number root with a multiplicity of 2.

if 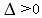DELTA%3E0 there are two real number roots.

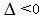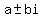
if DELTA%3C0 there is a conjugate pair of complex roots of the form a%2B-bi

I'll do the first one, and then you can do the rest:

x%5E2+%2B+6x+-+7+=+0

Here, a=1, b=6, and c=-7, so DELTA=6%5E2-4%281%29%28-7%29=36%2B28=64%3E0 so there are two real number roots.

Simple as that. You can do the rest.

************************************
2. To be exactly correct, this problem is incorrectly stated. x cannot simultaneously be 1 AND -8. x=1 OR x=-8.

Here's the rule: a is a root of a polynomial equation if and only if x-a is a factor of the polynomial.

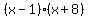Since x=1 OR x=-8 are roots of the desired quadratic, then x-1 and x%2B8 must be factors of the quadratic polynomial, so just multiply %28x-1%29%28x%2B8%29 and set the result equal to zero.

************************************

3. This one is answered in the discussion for problem 1 above.

************************************

4. No idea how to answer this one. You get zeros at -4 and 7, and a minimum value at 1.5 Your guess is as good as mine.