SOLUTION: how do you use the quadratic formula for 2a^2 - 46a + 252 = 0? please round to the nearest hundreth

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: how do you use the quadratic formula for 2a^2 - 46a + 252 = 0? please round to the nearest hundreth      Log On


   

Question 171868: how do you use the quadratic formula for 2a^2 - 46a + 252 = 0? please round to the nearest hundreth
Found 2 solutions by Alan3354, jim_thompson5910:
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
how do you use the quadratic formula for 2a^2 - 46a + 252 = 0? please round to the nearest hundreth
---------------------
2a^2 - 46a + 252 = 0
Divide by 2.
Always reduce when possible, it makes it easier to spot factors, and, if you do it by hand, it makes the numbers you deal with smaller.
a^2 - 23a + 126 = 0
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B-23x%2B126+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-23%29%5E2-4%2A1%2A126=25.

Discriminant d=25 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--23%2B-sqrt%28+25+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-23%29%2Bsqrt%28+25+%29%29%2F2%5C1+=+14
x%5B2%5D+=+%28-%28-23%29-sqrt%28+25+%29%29%2F2%5C1+=+9

Quadratic expression 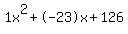1x%5E2%2B-23x%2B126 can be factored:
1x%5E2%2B-23x%2B126+=+%28x-14%29%2A%28x-9%29
Again, the answer is: 14, 9. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B-23%2Ax%2B126+%29

So it's 14 and 9. The solver always uses x, sub a for x.




Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!

2a%5E2-46a%2B252=0 Start with the given equation.


Notice we have a quadratic equation in the form of aa%5E2%2Bba%2Bc where a=2, b=-46, and c=252


Let's use the quadratic formula to solve for a


a+=+%28-b+%2B-+sqrt%28+b%5E2-4ac+%29%29%2F%282a%29 Start with the quadratic formula


a+=+%28-%28-46%29+%2B-+sqrt%28+%28-46%29%5E2-4%282%29%28252%29+%29%29%2F%282%282%29%29 Plug in a=2, b=-46, and c=252


a+=+%2846+%2B-+sqrt%28+%28-46%29%5E2-4%282%29%28252%29+%29%29%2F%282%282%29%29 Negate -46 to get 46.


a+=+%2846+%2B-+sqrt%28+2116-4%282%29%28252%29+%29%29%2F%282%282%29%29 Square -46 to get 2116.


a+=+%2846+%2B-+sqrt%28+2116-2016+%29%29%2F%282%282%29%29 Multiply 4%282%29%28252%29 to get 2016


a+=+%2846+%2B-+sqrt%28+100+%29%29%2F%282%282%29%29 Subtract 2016 from 2116 to get 100


a+=+%2846+%2B-+sqrt%28+100+%29%29%2F%284%29 Multiply 2 and 2 to get 4.


a+=+%2846+%2B-+10%29%2F%284%29 Take the square root of 100 to get 10.


a+=+%2846+%2B+10%29%2F%284%29 or a+=+%2846+-+10%29%2F%284%29 Break up the expression.


a+=+%2856%29%2F%284%29 or a+=++%2836%29%2F%284%29 Combine like terms.


a+=+14 or a+=+9 Simplify.


So the answers are a+=+14 or a+=+9