Question 169618: During the first part of a trip, a canoeist travels 37 miles at a certain speed. The canoeist travels 7 miles on the second part or the trip at a speed 5 mph slower. The total time for the trip is 4 hours. What is the speed on each part of the trip?
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! Your basic formula is  , distance equals rate times time.
For the first leg of the trip, the distance is 37 miles, and both the rate and time are unknown. Call them  and  , so:
Equation 1: 
For the second leg of the trip the the distance is 7 miles, and both the rate and time are unknown. Call them  and  , so:
Equation 2:  which can also be stated Equation 2a: 
We also know that:
Equation 3:  because the speed on the second leg was 5 mph slower.
And:
Equation 4:  because the total time equals 4 hours. This can also be stated Equation 4a: 
Substituting Equations 3 and 4a into Equation 1 yields:
Equation 5: 
And substituting Equation 2a into equation 5 yields:
Equation 6: 
Expand the binomial:
Collect terms:
Multiply by
Use the quadratic formula
Since 1136 = 16 * 71 and 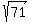 is irrational, reduce to:
Sinc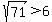e  , the 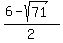 result is absurd because, presumably, the canoe never went backwards. Therefore, the rate of speed for the second leg of the trip is exactly 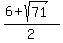 and the rate for the first leg of the trip is 
Use your calculator to determine 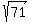if you want a numerical approximation for the answer, but remember to round off to the nearest whole number because all of your given values, i.e. the two distances and the total time were given as whole numbers.
Calculating the times for the indiviual legs and using these values to check the answer is left as an exercise for the student.
|
|
|
