SOLUTION: pls.help me solve the following quadratic equation by factoring: {{{2x^2-3x+1=0}}} {{{4x^2+9x=9}}} {{{2y^2+y=-11y}}} {{{y^2-7-44=0}}} {{{6x^2+11x-1=0}}} pls. submit your

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: pls.help me solve the following quadratic equation by factoring: {{{2x^2-3x+1=0}}} {{{4x^2+9x=9}}} {{{2y^2+y=-11y}}} {{{y^2-7-44=0}}} {{{6x^2+11x-1=0}}} pls. submit your       Log On


   

Question 162005: pls.help me solve the following quadratic equation by factoring:
2x%5E2-3x%2B1=0
4x%5E2%2B9x=9
2y%5E2%2By=-11y
y%5E2-7-44=0
6x%5E2%2B11x-1=0
pls. submit your answer as soon as possible i need to pass it tomorrow
im begging you pls..
Found 2 solutions by KnightOwlTutor, scott8148:
Answer by KnightOwlTutor(293) About Me  (Show Source):
You can put this solution on YOUR website!
2x%5E2-3x%2B1=0
We know that the last term must be 1
Set up the equation like this
it could be -1,-1 or 1,1
Because you have a negative middle term it is most likely -1,-1
(2x-1)(x-1)=0
Therefore the solution is x= 1/2 or 1 we need to make the equation=0 and the only way to accomplish this is to make one or both terms =0



4x%5E2%2B9x=9
We need to subtract 9 from both sides of the equation
4x^2+9x-9=0
We need to find two numbers that have a product of 9 the possibilities are 3,3
9,1
We have a negative number so we know that the product is -
We then need to know what 2 numbers give a product of 4
2,2 or 4,1
Let's set up the equation
using 3,3
(_x-3)(_x+3)
The middle terms need to add up to 9x Let's try 4 and 1
(4x-3)(x+3) The middle term for this problem is -3x+12x=9x
We have the correct factors
the solution is x=3/4 or -3


2y%5E2%2By=-11y
Here we add 11y to both sides of the equation
2y^2+y+11y=0
2y^2+12y=0
factor out 2
2(y^2+6)=0
y=sqrt6 i
remember that i=sqrt of -1

y%5E2-7-44=0
First we try to calculate the numbers that generate a product of 44
4,11 or 44,1
Let's try 4,11
(y-11)(y+4)
y =11 or -4

6x^2+11x-1=0
ax^2+bx+c=0 a=6 b=11 c=-1
Solved by pluggable solver: SOLVE quadratic equation with variable
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 6x%5E2%2B11x%2B-1+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%2811%29%5E2-4%2A6%2A-1=145.

Discriminant d=145 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28-11%2B-sqrt%28+145+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%2811%29%2Bsqrt%28+145+%29%29%2F2%5C6+=+0.0867995482326913
x%5B2%5D+=+%28-%2811%29-sqrt%28+145+%29%29%2F2%5C6+=+-1.92013288156602

Quadratic expression 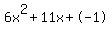6x%5E2%2B11x%2B-1 can be factored:
6x%5E2%2B11x%2B-1+=+6%28x-0.0867995482326913%29%2A%28x--1.92013288156602%29
Again, the answer is: 0.0867995482326913, -1.92013288156602. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+6%2Ax%5E2%2B11%2Ax%2B-1+%29





Use the quadratic formula

Answer by scott8148(6628) About Me  (Show Source):
You can put this solution on YOUR website!
2x^2-3x+1=0 __ (2x-1)(x-1)=0

4x^2+9x=9 __ 4x^2+9x-9=0 __ (4x-3)(x+3)=0

2y^2+y=-11y __ 2y^2+12y=0 __ 2y(y+6)=0

y^2-7-44=0 __ y^2-51=0 __ (y+sqrt(51))(y-sqrt(51))=0

6x^2+11x-1=0 __ not factorable