pls.help me solve the following quadratic equation by factoring:
 Multiply the
Multiply the  in front by the
in front by the 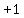 ,
getting
,
getting  . So we write down
. So we write down
 as the only way to find two factors of
as the only way to find two factors of  .
Next look at the sign of the last term
.
Next look at the sign of the last term 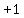 on the left. It is
on the left. It is 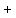 so beside
so beside  we write the sum
we write the sum  , and what it equals,
, and what it equals,  :.
:.

 We observe that the absolute
value of the coefficient of the middle term on the left of
We observe that the absolute
value of the coefficient of the middle term on the left of
 is
is  so we replace the
so we replace the  by
by
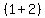 , so
, so
 becomes
becomes
 Now place the
Now place the  on the left of the
on the left of the 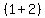 as
as
 Us the distributive property to multiply out
Us the distributive property to multiply out 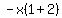 as
as  . So now we have:
. So now we have:
 Out of the first two terms on the left ONLY,
Out of the first two terms on the left ONLY, 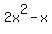 ,
we can factor out
,
we can factor out  , getting
, getting 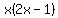 Out of the last two terms on the left ONLY,
Out of the last two terms on the left ONLY, 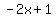 ,
we can factor out
,
we can factor out  , getting
, getting 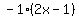 .
[Notice when the first of the last two terms begins
with a "-" sign, always take out a "-" term, which
will invariably change the sign of the second term.]
So we have
.
[Notice when the first of the last two terms begins
with a "-" sign, always take out a "-" term, which
will invariably change the sign of the second term.]
So we have
 Now we take out the parentheses
Now we take out the parentheses 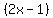 as a
common factor and leave the
as a
common factor and leave the  and the
and the  to put inside parentheses, like this:
to put inside parentheses, like this:
 Noqw we use the zero-factor principle where we
set each factor = 0:
Noqw we use the zero-factor principle where we
set each factor = 0:
 So the solution set is
So the solution set is  That's just the first one. If I have time I will come back
and finish the rest. So check this site later, for I will
probably do some more.
Edwin
That's just the first one. If I have time I will come back
and finish the rest. So check this site later, for I will
probably do some more.
Edwin



