Question 157251: I am given the zeros (ie. cross x axis at -3 and 4), and told the equation crosses the y axis at 48, how would I make a quadratic equation out of this?
Answer by nerdybill(7384)   (Show Source): (Show Source):
You can put this solution on YOUR website! I am given the zeros (ie. cross x axis at -3 and 4), and told the equation crosses the y axis at 48, how would I make a quadratic equation out of this?
.
Since the problem states that the quadratic crosses the x-axis at -3 and 4 we now KNOW two factors of the quadratic. So far, then, we have:
y = (x+3)(x-4)
.
Notice that to determine where a quadratic crosses the y-axis, set x=0 and solve for y:
y = (x+3)(x-4)
y = (0+3)(0-4)
y = (3)(-4)
y = -12
And, because the problem states that it "crosses the y axis at 48"...
To get it to 48, we ask ourself what do we multiply -12 with to get 48? And, the answer is -4.
.
So, now we have:
y=-4(x+3)(x-4)
y=-4(x^2-x-12)
y=-4x^2+4x+48 (this is what they are looking for)
.
Here's the quadratic solution:
| Solved by pluggable solver: SOLVE quadratic equation with variable |
Quadratic equation  (in our case (in our case  ) has the following solutons: ) has the following solutons:

For these solutions to exist, the discriminant  should not be a negative number. should not be a negative number.
First, we need to compute the discriminant  : :  . .
Discriminant d=784 is greater than zero. That means that there are two solutions:  . .


Quadratic expression 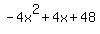 can be factored: can be factored:

Again, the answer is: -3, 4.
Here's your graph:
 |
|
|
|