Question 156612: A wire 350 mm long is cut in two pieces. The first piece is shaped into a circle, and the second piece is shaped into a square. Both shapes have the same area. What is the length of each wire?
I have no idea where to even start on this problem, so please help!
Found 2 solutions by gonzo, solver91311:
Answer by gonzo(654)   (Show Source): (Show Source):
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! One of the pieces is x mm long and the other is 350 - x mm.
Let's take the first one and make a circle. That means the circumference of the circle is x, but we know that the circumference of a circle is  , so the radius of the circle must be , so the radius of the circle must be  . The area of a circle is . The area of a circle is  , so the area of this circle must be , so the area of this circle must be 
Since the piece used for the circle was x, the perimeter of the square must be 350-x. Therefore the measure of one side of the square must be 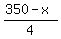 , and then the area of the square must be , and then the area of the square must be 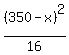 or or 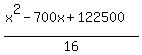 . .
We are given that the two areas are equal, so:

A little manipulation gets us to:

which is a quadratic in x with  , ,  , and , and 
So, 
I'll let you deal with this arithmetic horror because I'm WAY too lazy. But one of the roots will be negative and you can exclude it as extraneous. Remember the root of this equation is the length of the piece of wire used to make the circle, you have to subtract from 350 to get the length of the wire used for the square. Good luck. Unfortunately, the Eighth Amendment to the Constitution of the United States only prevents the Federal Government, not Math Teachers, from inflicting cruel and unusual punishments.
|
|
|