Question 156148: Solve
15x^4-31x^2+10=0
The solution of x= ??
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let  . So . So  . In short, . In short, 
 Start with the given equation Start with the given equation
 Plug in Plug in  and and 
| Solved by pluggable solver: Quadratic Formula |
Let's use the quadratic formula to solve for z:
Starting with the general quadratic

the general solution using the quadratic equation is:

So lets solve  ( notice ( notice  , ,  , and , and  ) )
 Plug in a=15, b=-31, and c=10 Plug in a=15, b=-31, and c=10
 Negate -31 to get 31 Negate -31 to get 31
 Square -31 to get 961 (note: remember when you square -31, you must square the negative as well. This is because Square -31 to get 961 (note: remember when you square -31, you must square the negative as well. This is because  .) .)
 Multiply Multiply 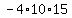 to get to get 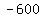
 Combine like terms in the radicand (everything under the square root) Combine like terms in the radicand (everything under the square root)
 Simplify the square root (note: If you need help with simplifying the square root, check out this solver) Simplify the square root (note: If you need help with simplifying the square root, check out this solver)
 Multiply 2 and 15 to get 30 Multiply 2 and 15 to get 30
So now the expression breaks down into two parts
 or or 
Lets look at the first part:

 Add the terms in the numerator Add the terms in the numerator
 Divide Divide
So one answer is

Now lets look at the second part:

 Subtract the terms in the numerator Subtract the terms in the numerator
 Divide Divide
So another answer is

So our solutions are:
 or or 
|
Remember, we let  . So this means that . So this means that
 or or 
Take the square root of both sides for each case (remember the "plus/minus")
 , ,  , ,  , or , or 
Rationalize the denominator (if necessary)
 , ,  , ,  , or , or 
--------------------------------------
Answer:
So the solutions are
 , ,  , ,  , or , or 
|
|
|