SOLUTION: I am trying to find b^2-4ac and the number of real solutions for the equation 16-24x+9x^2=0. If I put it in standard form ax^2 + ax + a = 0 a=-9 b=24 c=-16 b^2-4ac= 24^2

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: I am trying to find b^2-4ac and the number of real solutions for the equation 16-24x+9x^2=0. If I put it in standard form ax^2 + ax + a = 0 a=-9 b=24 c=-16 b^2-4ac= 24^2       Log On


   

Question 151472: I am trying to find b^2-4ac and the number of real solutions for the equation 16-24x+9x^2=0.

If I put it in standard form ax^2 + ax + a = 0
a=-9 b=24 c=-16
b^2-4ac= 24^2 - 4(-9)(-16)=576-576= 0
So: when the discriminat equals 0 there should be only one solution correct? But how do I find that 1 solution?
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
16-24x%2B9x%5E2=0 Start with the given equation.


9x%5E2-24x%2B16=0 Rearrange the terms.


From 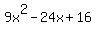9x%5E2-24x%2B16 we can see that a=9, b=-24, and c=16


D=b%5E2-4ac Start with the discriminant formula.


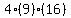D=%28-24%29%5E2-4%289%29%2816%29 Plug in a=9, b=-24, and c=16


D=576-4%289%29%2816%29 Square -24 to get 576


D=576-576 Multiply 4%289%29%2816%29 to get %2836%29%2816%29=576


D=0 Subtract 576 from 576 to get 0


Since the discriminant is equal to zero, this means that there is one real solution.


So you are correct. However, I'm not sure where you got a=-9 b=24 c=-16 from.


---------------------------------------

To find the one solution, you have 2 options

Option # 1 Quadratic Formula (preferred method)

9x%5E2-24x%2B16=0 Start with the given equation.


Notice we have a quadratic equation in the form of ax%5E2%2Bbx%2Bc where a=9, b=-24, and c=16


Let's use the quadratic formula to solve for x


x+=+%28-b+%2B-+sqrt%28+b%5E2-4ac+%29%29%2F%282a%29 Start with the quadratic formula


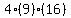x+=+%28-%28-24%29+%2B-+sqrt%28+%28-24%29%5E2-4%289%29%2816%29+%29%29%2F%282%289%29%29 Plug in a=9, b=-24, and c=16


x+=+%2824+%2B-+sqrt%28+%28-24%29%5E2-4%289%29%2816%29+%29%29%2F%282%289%29%29 Negate -24 to get 24.


x+=+%2824+%2B-+sqrt%28+576-4%289%29%2816%29+%29%29%2F%282%289%29%29 Square -24 to get 576.


x+=+%2824+%2B-+sqrt%28+576-576+%29%29%2F%282%289%29%29 Multiply 4%289%29%2816%29 to get 576


x+=+%2824+%2B-+sqrt%28+0+%29%29%2F%282%289%29%29 Subtract 576 from 576 to get 0


x+=+%2824+%2B-+sqrt%28+0+%29%29%2F%2818%29 Multiply 2 and 9 to get 18.


x+=+%2824+%2B-+0%29%2F%2818%29 Take the square root of 0 to get 0.


x+=+%2824+%2B+0%29%2F%2818%29 or x+=+%2824+-+0%29%2F%2818%29 Break up the expression.


x+=+%2824%29%2F%2818%29 or x+=++%2824%29%2F%2818%29 Combine like terms.


x+=+4%2F3 or x+=+4%2F3 Simplify.


So our answer is x+=+4%2F3 (with a multiplicity of 2)



Option # 2 Factoring:

9x%5E2-24x%2B16=0 Start with the given equation

%283x-4%29%283x-4%29=0 Factor the left side (note: if you need help with factoring, check out this solver)



Now set each factor equal to zero:
3x-4=0 or 3x-4=0

x=4%2F3 or x=4%2F3 Now solve for x in each case


Since we have a repeating answer, our only answer is x=4%2F3