Question 143952: A designer, attempting to arrange the characters of his artwork in the form of a square grid with equal number of rows and columns, found that 24 characters were left out. When he tried to add one more row and column, he found that he was short of 25 characters. Can you find the number of characters used by the designer?
Found 2 solutions by stanbon, vleith:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! A designer, attempting to arrange the characters of his artwork in the form of a square grid with equal number of rows and columns, found that 24 characters were left out. When he tried to add one more row and column, he found that he was short of 25 characters. Can you find the number of characters used by the designer?
--------------
Let the number of rows/columns in the 1st square be "x".
--------------
EQUATIONS:
# of characters = x^2+24
# of characters = (x+1)(x+1)-25
-------------
x^2+24 = (x+1)^2-25
x^2+24 = x^2+2x+1-25
24 = 2x-24
2x = 48
x = 24
--------------------
# of characters = 24^2 = 576
=================================
Cheers,
Stan H.
Answer by vleith(2983)   (Show Source): (Show Source):
You can put this solution on YOUR website! The first square had 24 left over pieces.
Adding a row and column, puts 12 across one row and 13 in the column (since the corner piece is part of both the row and column).
We are told that configuration leaves us 25 pieces short of a square. We will need 13 pieces to compete the row and 12 pieces to complete the column. At that point, we would have a square that is 25 on each side.
So he has  or or 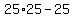 = 600 = 600
|
|
|