SOLUTION: The width of a rectangle is 4 cm less than the length. The area is 350cm^2. Find the length and width.

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: The width of a rectangle is 4 cm less than the length. The area is 350cm^2. Find the length and width.      Log On


   

Question 141566This question is from textbook
: The width of a rectangle is 4 cm less than the length. The area is 350cm^2. Find the length and width. This question is from textbook

Answer by jojo14344(1513) About Me  (Show Source):
You can put this solution on YOUR website!
Sure amigo!
First, Area of rectangle (A)= (Length)(Width)-------- eqn 1
But, Width(W) is 4cm less than the Length(L), so W= L-4, ---- eqn 2, then
A= (L-4)(L)
350=L^2-4L
L^2-4L-350=0
Let's assigned "L" to "x" and used quadratic formula, therefore
Solved by pluggable solver: SOLVE quadratic equation (work shown, graph etc)
Quadratic equation ax%5E2%2Bbx%2Bc=0 (in our case 1x%5E2%2B-4x%2B-350+=+0) has the following solutons:

x%5B12%5D+=+%28b%2B-sqrt%28+b%5E2-4ac+%29%29%2F2%5Ca

For these solutions to exist, the discriminant b%5E2-4ac should not be a negative number.

First, we need to compute the discriminant b%5E2-4ac: b%5E2-4ac=%28-4%29%5E2-4%2A1%2A-350=1416.

Discriminant d=1416 is greater than zero. That means that there are two solutions: +x%5B12%5D+=+%28--4%2B-sqrt%28+1416+%29%29%2F2%5Ca.

x%5B1%5D+=+%28-%28-4%29%2Bsqrt%28+1416+%29%29%2F2%5C1+=+20.8148877222268
x%5B2%5D+=+%28-%28-4%29-sqrt%28+1416+%29%29%2F2%5C1+=+-16.8148877222268

Quadratic expression 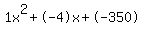1x%5E2%2B-4x%2B-350 can be factored:
1x%5E2%2B-4x%2B-350+=+%28x-20.8148877222268%29%2A%28x--16.8148877222268%29
Again, the answer is: 20.8148877222268, -16.8148877222268. Here's your graph:
graph%28+500%2C+500%2C+-10%2C+10%2C+-20%2C+20%2C+1%2Ax%5E2%2B-4%2Ax%2B-350+%29


Of course we use the positive (+) value which is 20.8148877 cm= x = L (Length)
So the Width (W) we go back eqn 2, W=L-4= 20.8148877 - 4
W=16.8148877 cm
In doubt, simply go back to eqn 1,
A=(L)(W)
350 sq cm= (20.8148877)(16.8148877)
350 sq cm= 350 sq cm, cool!
Thank you,
Jojo