SOLUTION: Can someone solve the equations for these. (3,1),(1,3) and (0,3),(5,0)to show me the answer? Thanks!

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: Can someone solve the equations for these. (3,1),(1,3) and (0,3),(5,0)to show me the answer? Thanks!       Log On


   

Question 135644: Can someone solve the equations for these. (3,1),(1,3) and (0,3),(5,0)to show me the answer? Thanks!
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
Since you are asking to "solve" the equations, I am presuming that you want the solution set of the system of two equations. First, you have to derive the two equations.

Given two points, use the two-point form of the equation for a line:

y-y%5B1%5D=%28%28y%5B1%5D-y%5B2%5D%29%2F%28x%5B1%5D-x%5B2%5D%29%29%28x-x%5B1%5D%29

Substitute the values for the x- and y-coordinates into the equation and do the appropriate arithmetic. I'll set it up for your first set of points.

Let (3,1) be point 1, and (1, 3) be point 2. So:

x%5B1%5D=3 because P1: (red%283%29,1)
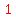y%5B1%5D=1 because P1: (3,red%281%29)

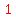x%5B2%5D=1 because P2: (red%281%29,3)
y%5B2%5D=3 because P2: (1,red%283%29)

y-1=%28%281-3%29%2F%283-1%29%29%28x-3%29

Now, do the arithmetic and then arrange the equation into standard form: ax%2Bby=c and you are done. Follow the same procedure for your other set of points.

Once you have derived the two equations, then we can go about the process of solving the system. Write back with your solution and I'll let you know if you have done the equation derivations correctly. Then we can talk about the solution to the system. Hint: Pay careful attention when adding signed numbers.