Question 133462: A chain store manager has been told by the main office that daily profit, P, is related to the number of clerks working that day, x, according to the equation P=-25x^2+300x. What number of clerks will maximize the profit, and what is the maximum possible profit?
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! This is a quadratic equation of the form  and the graph of this relationship is a parabola. In this case a = -25, b = 300, and c = 0.
Since you put this question in the Algebra: Quadratic Equations section, I'll show you the algebra method to solve it. If you actually need the calculus method, write back and I'll show you that way.
A parabola with a lead coefficient that is less than zero opens downward, hence the vertex of the parabola is a maximum point. The x-coordinate of the vertex of a parabola of the form is given by 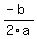 and the y-coordinate is just the value of the function evaluated at the x-coordinate.
For your function, the vertex is at the point (x,y) where
 and
So, the maximum profit will be achieved when 6 clerks are working, and that profit is 900 (anybody's guess as to whether that is dollars, thousands of dollars, euros, yen, or some other currency)
Following is a graphical illustration of the situation:
|
|
|
