SOLUTION: How do you determine the min or max of -3x^2+24x?

Click here to see ALL problems on Quadratic Equations

Question 133084: How do you determine the min or max of -3x^2+24x?
Found 2 solutions by jim_thompson5910, vleith:
Answer by jim_thompson5910(35256) (Show Source):
You can put this solution on YOUR website!
To find the min/max of , we need to find the vertex. However, we first need to find the axis of symmetry

To find the axis of symmetry, use this formula:

From the equation we can see that a=-3 and b=24

Plug in b=24 and a=-3

Multiply 2 and -3 to get -6

Reduce

So the axis of symmetry is

So the x-coordinate of the vertex is . Lets plug this into the equation to find the y-coordinate of the vertex.

Lets evaluate

Start with the given polynomial

Plug in

Raise 4 to the second power to get 16

Multiply 3 by 16 to get 48

Multiply 24 by 4 to get 96

Now combine like terms

So the vertex is (4,48)

Now since the leading coefficient is -3, this means that the parabola opens down. So at the vertex there is a maximum. Also, this means that the max is which occurs at

Answer by vleith(2983) (Show Source):
You can put this solution on YOUR website!
There are many ways to find the max/min. Not sure what tools you have handy, but you can:
1) Use a graphing calculator
2) Use an online tool like Geogebra
3) You can grind it out using trial and error
4) You can use algebra to help
5) Calculus makes it very easy.
I'll assume 1, 2 and 5 are not options for you. I am not into griding out answers. So let's use algebra.
Looking at the function 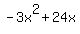, we can see that it represents a parabola. Given that the high order coefficient is negative, we know the parabola 'opens down'. Thus we are looking for a maximum.

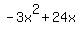
If we set the function equal to zero, we can find the places where the parabola intersects the x axis (where the value of y = 0).
By factoring the function, we see it can be represented as

So, when either factor is 0, the result is 0. Thus
x = 0 yields a result of zero AND x = 8 yields a result of zero.
So now we have two points on the parabola. In this case, those two points also happen to be reflections across the parabola's line if symmetry. So, what line lies halfway between (0,0) and (8,0) ?? Correct, x = 4.
So the value of x where the maximum occurs is 4. Solving yields

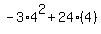
Which is the point (4,48)