Question 132906: While I can solve basic quadratic equations I am having problems figuring out how to solve the equations where you complete the square when ax^2+bx+c is equal to a number other than 0. For example:
-2.2x^2-7.4x+0.7=0.8
Answer by edjones(8007)   (Show Source): (Show Source):
You can put this solution on YOUR website! -2.2x^2-7.4x+0.7=0.8
-2.2x^2-7.4x-0.1=0
This problem is diabolical.
Luckily we have a solver to show you how to do it.
Of course, in the real world, if we were not forced to use completing the square method we would use the quadratic formula after multiplying both sides of the equation on the second line by -10.
.
Ed
| Solved by pluggable solver: COMPLETING THE SQUARE solver for quadratics |
Read this lesson on completing the square by prince_abubu, if you do not know how to complete the square.
Let's convert  to standard form by dividing both sides by -2.2: to standard form by dividing both sides by -2.2:
We have:  .
What we want to do now is to change this equation to a complete square .
What we want to do now is to change this equation to a complete square  . How can we find out values of somenumber and othernumber that would make it work? . How can we find out values of somenumber and othernumber that would make it work?
Look at  : :  . Since the coefficient in our equation . Since the coefficient in our equation  that goes in front of x is 3.36363636363636, we know that 3.36363636363636=2*somenumber, or that goes in front of x is 3.36363636363636, we know that 3.36363636363636=2*somenumber, or  . So, we know that our equation can be rewritten as . So, we know that our equation can be rewritten as 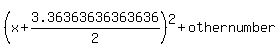 , and we do not yet know the other number. , and we do not yet know the other number.
We are almost there. Finding the other number is simply a matter of not making too many mistakes. We need to find 'other number' such that 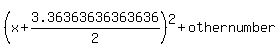 is equivalent to our original equation is equivalent to our original equation  . .

The highlighted red part must be equal to 0.0454545454545455 (highlighted green part).
 , or , or  . .
So, the equation converts to  , or , or  . .
Our equation converted to a square 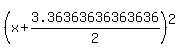 , equated to a number (2.78305785123967). , equated to a number (2.78305785123967).
Since the right part 2.78305785123967 is greater than zero, there are two solutions:

, or




Answer: x=-0.0135682451361301, -3.35006811850023.
|
|
|
|