Question 130665: Steven invests $2000 into a GIC which will double every five years, wheras Dana invests $1000 into a GIC which will triple evry three years. How many years will pass before they have the same amount of money?
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website! Steven invests $2000 into a GIC which will double every five years, wheras Dana invests $1000 into a GIC which will triple evry three years. How many years will pass before they have the same amount of money?
The rule is:
 We will assume the interest accrues once yearly, so n = 1
and the formula becomes
We will assume the interest accrues once yearly, so n = 1
and the formula becomes

 So for Steven, P = 2000, so the amount A, in t years, is
So for Steven, P = 2000, so the amount A, in t years, is
 Steven's GIC doubles every five years,
So we substitute t = 5, and A = 4000 (double 2000),
so we can solve for r:
Steven's GIC doubles every five years,
So we substitute t = 5, and A = 4000 (double 2000),
so we can solve for r:
 Divide both sides by 2000
Divide both sides by 2000
 Take the 5th root of both sides:
Take the 5th root of both sides:
 Simplifying the right side:
Simplifying the right side:
 Solving for r:
Solving for r:
 Substituting that into
Substituting that into

 or
or
 This is the formula for Steven's amount A in t years.
---------------------------------------------
Now we do exactly the same thing with Dana's
GIC.
This is the formula for Steven's amount A in t years.
---------------------------------------------
Now we do exactly the same thing with Dana's
GIC.
 Now for Dana, P = 1000, so the amount A, in t years, is
Now for Dana, P = 1000, so the amount A, in t years, is
 DANA's GIC triples every three years,
So we substitute t = 3, and A = 3000 (triple 1000),
so we can solve for r:
DANA's GIC triples every three years,
So we substitute t = 3, and A = 3000 (triple 1000),
so we can solve for r:
 Divide both sides by 1000
Divide both sides by 1000
 Take the cube root of both sides:
Take the cube root of both sides:
 Simplifying the right side:
Simplifying the right side:
 Solving for r:
Solving for r:
 Substituting that into
Substituting that into

 or
or
 This is the formula for Dana's amount A in t years.
-------------------------------
So to find out when they have an equal amount, we
set their two A's equal, and solve for t:
This is the formula for Dana's amount A in t years.
-------------------------------
So to find out when they have an equal amount, we
set their two A's equal, and solve for t:
 and and 
 Divide both sides by 1000
Divide both sides by 1000
 Change the roots to fractional exponentials of their radicands:
Change the roots to fractional exponentials of their radicands:
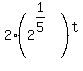 = = 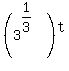 Multiply inner exponents by outer exponents
Multiply inner exponents by outer exponents
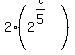 = = 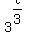 Write the first
Write the first  as as 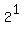
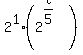 = = 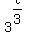 Change the exponent
Change the exponent  to to  so you
can add exponents on the left: so you
can add exponents on the left:
 = = 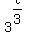 Add exponents:
Add exponents:
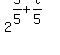 = = 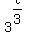
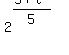 = = 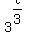
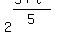 = = 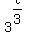 Raise both sides to the 15th power
Raise both sides to the 15th power
 = = 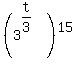 Multiply inner exponents by outer exponents:
Multiply inner exponents by outer exponents:
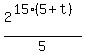 = = 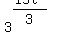 Cancel 5 into 15 on left and 3 into 15 on the right:
Cancel 5 into 15 on left and 3 into 15 on the right:
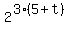 = = 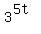
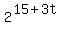 = = 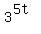 Take the log (either log10 or ln) of both sides
Take the log (either log10 or ln) of both sides
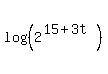 = = 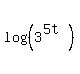 Use the rule of logs
Use the rule of logs 
 = =  Replace
Replace 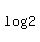 by by  and replace and replace 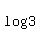 by by 
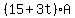 = = 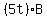
 = = 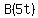
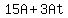 = = 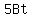 Isolate the terms in t on the right
Isolate the terms in t on the right
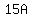 = = 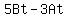 Factor out t on the right:
Factor out t on the right:
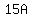 = = 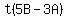 Divide both sides by
Divide both sides by 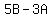
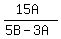 = =  Now replace
Now replace  by by 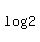 and replace
and replace  by by 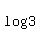
 = =  Use calculator to get right side
Use calculator to get right side
 = = 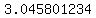 So the answer is just after 3 years.
Edwin
So the answer is just after 3 years.
Edwin
|
|
|