SOLUTION: I am supposed to "Solve each quadratic equation by completing the square. Leave your answer in radical form." I'm not really sure what the radical form is. I don't even know if thi

Algebra ->  Quadratic Equations and Parabolas  -> Quadratic Equations Lessons  -> Quadratic Equation Lesson -> SOLUTION: I am supposed to "Solve each quadratic equation by completing the square. Leave your answer in radical form." I'm not really sure what the radical form is. I don't even know if thi      Log On


   

Question 130272This question is from textbook Discovering Algebra
: I am supposed to "Solve each quadratic equation by completing the square. Leave your answer in radical form." I'm not really sure what the radical form is. I don't even know if this question falls under the section of quadratic equation or radicals. My textbook says I need to complete the square or something. The equation is x%5E2-4x-8=0. I tried to solve it symbollically (I think..) and I: added the 8 to the zero, square-rooted the whole thing and somehow I ended up with x-4x=_%2B4. I'm not sure if I'm done or not... Please help! This question is from textbook Discovering Algebra

Found 2 solutions by Earlsdon, solver91311:
Answer by Earlsdon(6294) About Me  (Show Source):
You can put this solution on YOUR website!
Solve by completing the square:
x%5E2-4x-8+=+0
Here's how you do "completing the square"
First, add 8 to both sides.
x%5E2-4x+=+8 Now, add the square of half the x-coefficient, that's %284%2F2%29%5E2+=+4 to both sides of the equation.
x%5E2-4x%2B4+=+8%2B4 Factor the left side and simplify the right side.
%28x-2%29%28x-2%29+=+12 So there's the square on the left side, see it?
%28x-2%29%5E2+=+12 Now take the square root of both sides.
x-2+=+sqrt%2812%29 Plus or minus. Now add 2 to both sides.
x+=+2%2B-sqrt%2812%29 The right side can be simplified because:sqrt%2812%29+=+sqrt%284%2A3%29 = 2sqrt%283%29, so...
x+=+2%2B2sqrt%283%29 or x+=+2-2sqrt%283%29 This is in "radical form"
Leaving the answer in "radical form" simply means don't take the square root of the answer but leave it with the square root (radical) symbol.

Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
Let's start from where you are with this right now and work backwards.

You said that sqrt%28x%5E2-4x%29=sqrt%288%29, and therefore x-4x=4 or x-4x=-4

If sqrt%288%29=4 then 8+=+4+%2A+4. We know that isn't true, so the right side of your result is certainly incorrect. x-4x=-3x and %28-3x%29%5E2=9x, and this is only true for two values of x (specifically 1 and -1). Therefore, the right side of your result is also incorrect in general.

So let's go back one more step, the one before you took the square root of both sides. x%5E2-4x=8 is a good start. But what you need to do now is 'complete the square' That means that you are going to add a constant to both sides of the equation that makes that left side a perfect square. The process for this is actually simpler than it sounds.

Step 1: Divide both sides of your equation by the coefficient on the x%5E2 term. This is very easy for your problem because the x%5E2 term coefficient is 1, and you don't have to change anything.

Step 2: Take the coefficient on the x term and divide it by 2. Your problem, the coefficient is -4, divided by 2 is -2.

Step 3: Square the result of step 2. For your problem, %28-2%29%5E2=4.

Step 4: Add the result of step 3 to both sides of your equation. Your problem: x%5E2-4x%2B4=12

Step 5: Now that the left side of the equation is a perfect square, you can take the square root of both sides. First note that 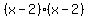x%5E2-4x%2B2=%28x-2%29%5E2 (You can use FOIL on %28x-2%29%28x-2%29 to verify that fact)

%28x-2%29%5E2=12, so:

x-2=sqrt%2812%29 or x-2=-sqrt%2812%29

x=2%2B-sqrt%2812%29

That is a representation of the solution set, in radical form (a radical is the square root sign). However, there is one more simplification step that you can take. Remember that sqrt%28ab%29=sqrt%28a%29%2Asqrt%28b%29. 12 = 4 * 3, so sqrt%2812%29=sqrt%284%29sqrt%283%29=2%2Asqrt%283%29. That means your final answer is:

x=2%2B2%2Asqrt%283%29 or x=2-2%2Asqrt%283%29

Check the answer. If we did the work correctly, we should be able to substitute either of these values for x into the original equation and have it be a true statement.

x%5E2-4x-8=0

%282%2B2%2Asqrt%283%29%29%5E2-4%282%2B2%2Asqrt%283%29%29-8=0

%284%2B8%2Asqrt%283%29%2B12%29-%288%2B8%2Asqrt%283%29%29-8=0

16%2B8%2Asqrt%283%29-16-8%2Asqrt%283%29=0

0=0

So, the first answer works. I'll leave it to you to prove the second one. Or just trust me.