Question 129818This question is from textbook
: can you assist me to solved this linear equation by graphing
x+2y=5
x-y=2
how do I determin wheather the following has one solution, no solution or many solution. : y=-x+2
3x+3y=6
use substitution to solved: 2x+y=7
5x-2y=7
Thank you for your assistant
This question is from textbook
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! 1) To solve a system by graphing, you need to graph each of the lines on the same coordinate system and then find the point of intersection.
2) First, put both of the equations in standard form: 
 : Add x to both sides
The second equation is already in standard form, so your two equations are:
Compare the coefficients on one of the variables. The coefficients on the x variable are 1 and 3. If you multiply the first equation by -3, then the coefficients on x will be additive inverses, namely -3 and 3.
Now add the two equations term by term:
We got the result that  , a statement that is always true. That means that ANY ordered pair that will satisfy one of the equations will also satisfy the other, hence the solution set for this system has an infinite number of elements.
In contrast, what if we had a similar system, say:
Let's do the same process, multiply equation 1 by -3:
And add the two equations:
Now we have the always false statement  . In this case there is no ordered pair (x,y) that satisfies both equation simultaneously. The solution set to this system is therefore empty.
Graphically speaking, the problem as stated gave you two different forms of the equation of the same line, so all of the points of one are in common with all of the points of the other. In my modified example, we have two equations that represent parallel lines. Parallel lines have no point of intersection, so there is no solution to the system.
Original equations:
You can only see one line on the graph because the two lines are the same line:
Modified equations:
You can see that the two lines never intersect:
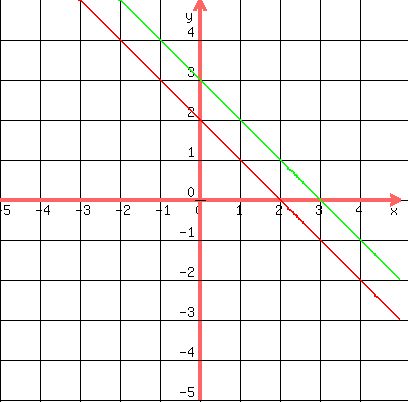
3)
To solve by substitution, the first step is to solve (re-arrange) one of the equations to get an expression for one of the variables in terms of the other. Let's perform this process on the first equation and solve for y:
: Add -2x to both sides
Now we can take this expression for y and substitute it (put it in place of) the y in the second equation:
 : Distribute the -2
 : Add 14 to both sides and combine like terms
Now that we have a value for x, we can substitute that into either of the original equations:
And the solution set is the ordered pair: ( ,)
Check
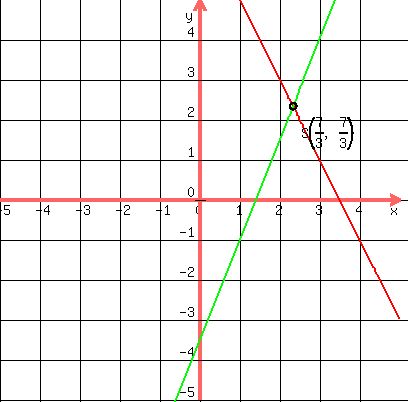
Super-double-plus extra credit:
On the graph above, which line is a graph of which equation? Triple credit if you do it in your head just looking at the equations.
|
|
|
