Question 129060: The manager of an 80 unit apartment complex is trying to deceide what rent to charge. Experience has shown that at a rent of $200.00 all the units will be full but with one additional unit will remain vacant f0r each $20.00increase. Find the # of occupied unit if the total revenue is $20,020.
This is the problem I am trying to solve, however I am not clear on how or where to start it. If you could possibly show me the steps I would greatly appericate it. Thank you
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! Let x be the number of occupied units. Then 80 - x is the number of unoccupied units.
The rental fee is 200 plus 20 times the number of unoccupied units, so:
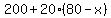 , which simplifies to:
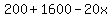
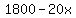
This is the amount charged per apartment, and there are x occupied apartments, so the total revenue is:
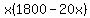 and that is equal to $20,020.
So:
Divide by -20:
You can factor this (the prime factors of 1001 are 7, 11, and 13), or use the quadratic formula, whichever you prefer, but the roots come out to be  and  ,
So, if the rental fee is 200 + 20(3) = 260 (3 unoccupied units), then the total revenue is 77 * 260 = 20020.
But if the rental fee is 200 + 20(67) = 1540, then the total revenue is 13 * 1540, also = 20020.
The second root presumes that the relationship of rent to unoccupied units is linear across the entire range of possibilities, which I suspect is not the case in real life.
|
|
|
