Question 127617: The publisher of a magazine that has a circulation of 80,000 and sells for 1.60$ a copy decides to raise the price of the magazine because of costs. By surveying the readers, he finds that he will lose 10,000 readers for each .40 $ increase. What price per copy maximizes growth?
TYVM for ANY answers =D
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! The publisher of a magazine that has a circulation of 80,000 and sells for 1.60$ a copy decides to raise the price of the magazine because of costs. By surveying the readers, he finds that he will lose 10,000 readers for each .40 $ increase. What price per copy maximizes growth?
;
By growth do they mean maximize revenue, if that is the case we can do it this way;
:
Let x = no. of 40 cent increases
and
Let x = no. of 10,000 reader decreases
:
Revenue = price * no. of readers
:
R = (1.60 + .40x) * (80000 - 10000x)
FOIL
R = 128000 - 16000x + 32000x - 4000x^2
As a quadratic
-4000x^2 + 16000x + 128000 = 0
:
Simplify, divide equation by 4000
-x^2 + 4x + 32 = 0
:
Max will occur at the axis of symmetry: x = -b/(2a); Here: a=-1; b=4
x = 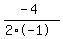
x = +2
:
That would be 2 ea .40 increases for a cost of 2.40 per copy
and
2 ea 10000 readers lost for a total 60000 readers
:
Revenue = 60000 * 2.40 = $144,000 (maximum)
:
If you graphed it:

Multiply the y value by 4000 to get the actual revenue
|
|
|